题目内容
16.化简:($\frac{x}{x-1}$-x)÷$\frac{x-2}{x^2-2x+1}$.分析 先算括号里面的,分母要因式分解,再算除法即可.
解答 解:原式=[$\frac{x}{x-1}$-$\frac{x(x-1)}{x-1}$]÷$\frac{x-2}{x2-2x+1}$,
=$\frac{x-x(x-1)}{x-1}$×$\frac{x2-2x+1}{x-2}$,
=$\frac{2x-x2}{x-1}$×$\frac{x2-2x+1}{x-2}$,
=$\frac{x(2-x)}{x-1}$×$\frac{(x-1)2}{x-2}$,
=-x(x-1),
=-x2+x.
点评 本题考查了分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目




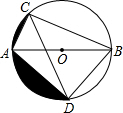 如图,AB为⊙O的直径,弦AC=3,∠ABC=30°,∠ACB的平分线交⊙O于点D.
如图,AB为⊙O的直径,弦AC=3,∠ABC=30°,∠ACB的平分线交⊙O于点D.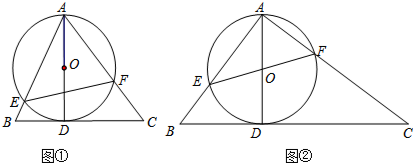
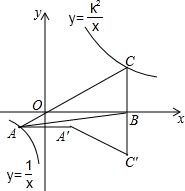 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}$(x>0,k是不等于0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,交于x轴于点B,连结AB,AA′,A′C′.若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}$(x>0,k是不等于0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,交于x轴于点B,连结AB,AA′,A′C′.若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于( )