题目内容
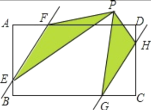
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,在AD上截取AE=AB,连接BE,EO,并求∠BEO的角度(要求:尺规作图,保留痕迹,不写作法)

【答案】作图见详解,∠BEO=30°.
【解析】
以A为圆心,以AB长为半径作圆,交AD于E.先证明△AOB是等边三角形,进而证明△AOE是等腰三角形,求出∠AEO=![]() ,再求出∠AEB=45°,问题得解.
,再求出∠AEB=45°,问题得解.
解:∵四边形ABCD是矩形,
∴∠BAE=90°,AC、BD相等且互相平分,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO, ∠BAO=60°,
∵AE=AB,
∴AE=AO, ∠EAO=∠BAE-∠BAO=30°,
∴∠AEO=![]()
∵∠BAE=90°,AE=AB,
∴∠AEB=∠ABE=45°,
∴∠BEO=∠AEO-∠AEB=30°.


练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目