题目内容
直线y=x+1与直线y=2x-3的交点坐标是
- A.(-2,-1)
- B.(4,5)
- C.(-4,-3)
- D.(2,3)
B
分析:求两条直线的交点,可联立两函数的解析式,所得方程组的解即为两个函数的交点坐标.因此本题需联立y=x+1,y=2x-3;通过解方程组,可求出它们的交点坐标.
解答:联立两函数的解析式有: ,
,
解得 ,
,
则直线y=x+1与直线y=2x-3的交点坐标是(4,5).
故选B.
点评:方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.
分析:求两条直线的交点,可联立两函数的解析式,所得方程组的解即为两个函数的交点坐标.因此本题需联立y=x+1,y=2x-3;通过解方程组,可求出它们的交点坐标.
解答:联立两函数的解析式有:
 ,
,解得
 ,
,则直线y=x+1与直线y=2x-3的交点坐标是(4,5).
故选B.
点评:方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
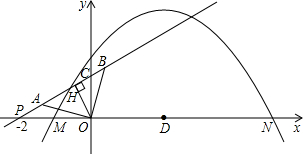 E点,直线NE与直线AB的交点G是否总满足PB•PG<10
E点,直线NE与直线AB的交点G是否总满足PB•PG<10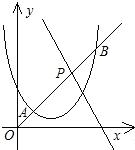 已知抛物线y=x2-2x+6-m与直线y=-2x+6+m,它们的一个交点的纵坐标是4.
已知抛物线y=x2-2x+6-m与直线y=-2x+6+m,它们的一个交点的纵坐标是4. (2013•威海)如图,在平面直角坐标系中,直线y=
(2013•威海)如图,在平面直角坐标系中,直线y=