Question

根据下表中关于二次函数y=ax²+bx+c的自变量x与函数y的对应值，可判断二次函数的图象与x轴

x	…	-1	0	1	2	…
y	…	-1		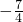-2		…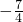

1. A.
   只有一个交点
2. B.
   有两个交点，且它们分别在y轴两侧
3. C.
   有两个交点，且它们均在y轴同侧
4. D.
   无交点

Answer 1

B
分析：利用二次函数y=ax²+bx+c的自变量x与函数y的对应值．
解答：根据表中的二次函数y=ax²+bx+c的自变量x与函数y的对应值，可以发现当x=0，x=2时，y的值都等于-＜0，
又根据二次函数的图象对称性可得：x=1是二次函数y=ax²+bx+c的对称轴，此时y有最小值-2，
再根据表中的数据，可以判断出y=0时，x＜-1或x＞2，
因此判断该二次函数的图象与x轴有两个交点，且它们分别在y轴两侧．
故选B．
点评：本题难度中等，考查二次函数与一元二次方程的关系．解决本题时能够画出图形，利用图象理解起来更为方便，数形结合是数学上一种重要的方法思想．