Question

【题目】在Rt△ABC中，∠ACB=90°，AB=9，cosA=，如果将△ABC绕着点C旋转至△A′B′C′的位置，使点B′落在∠ACB的角平分线上，A′B′与AC相交于点D，那么线段CD的长等于______．

Answer 1

【答案】30-12

【解析】

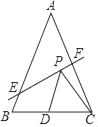
如图，作B′F⊥AC于F，A′E⊥AC于E．利用面积法构建方程即可解决问题.

如图，作B′F⊥AC于F，A′E⊥AC于E．

∵∠BCB′=∠ACB′=∠ACA′=45°，
∴△A′EC是等腰直角三角形，△FCB′是等腰直角三角形，
在Rt△ACB中，AB=9，cosA=，
∴AC=6，BC=3，
∴BF=CF=，EC=A′E=3，
∵S△A′B′C=×6×3=CD（3+），
∴CD=30-12.
故答案为30-12．