题目内容
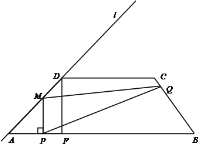
【题目】在△ABC中,AB=AC=10,sin∠BAC=![]() ,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
(1)求证:∠ABE=∠CAD.
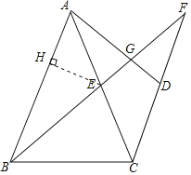
(2)如图,当点G在线段AD上时,求y关于x的函数解析式及定义域.
(3)若△DFG是直角三角形,求△CEF的面积.

【答案】(1)见解析;(2)y=![]() (0<x≤5
(0<x≤5![]() -5);(3)若△DFG是直角三角形,则△CEF的面积为15或
-5);(3)若△DFG是直角三角形,则△CEF的面积为15或![]() .
.
【解析】
(1)由CD∥AB知∠BAC=∠ECD,结合AE=CD,AB=AC证△DAC≌△EBA即可得;
(2)作EH⊥AB,先表示出S△ABE=![]() ABEH=3x,再证∴△CEF∽△AEB,得
ABEH=3x,再证∴△CEF∽△AEB,得![]() =(
=(![]() )2,据此可得答案;
)2,据此可得答案;
(3)由∠DFG=∠EBA<∠ABC知∠DFG不可能为直角,从而分∠DGF=90°和∠GDF=90°两种情况分别求解.
(1)∵CD∥AB,
∴∠BAC=∠ECD,
又∵AE=CD,AB=AC,
∴△DAC≌△EBA(SAS),
∴∠ABE=∠CAD;
(2)过点E作EH⊥AB,垂足为H,
由题意知CE=AC-AE=10-x,EH=AEsin∠CAB=![]() x,
x,
∴AH=![]() x,
x,
则S△ABE=![]() ABEH=
ABEH=![]() ×10×
×10×![]() x=3x,
x=3x,
∵CF∥BA,
∴△CEF∽△AEB,
∴![]() =(
=(![]() )2,即
)2,即![]() =
=![]() ,
,
∴y=![]() (0<x≤5
(0<x≤5![]() -5);
-5);
(3)∵∠DFG=∠EBA<∠ABC,
∴∠DFG不可能为直角,
①当∠DGF=90°时,∠EGA=90°,
由∠GAE=∠GBA知△GAE∽△GBA,
∴tan∠GBA=![]() =
=![]() =
=![]() ,
,
在Rt△EHB中,tan∠GBA=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:x=0(舍)或x=5,
∴S△CEF=![]() =15;
=15;
②当∠GDF=90°时,∠BAG=90°,
由①知△GAE∽△GBA,
则∠AEB=∠GEA=90°,
∴BE=ABsin∠BAC=10×![]() =6,AE=
=6,AE=![]() =8,CE=AC-AE=2,
=8,CE=AC-AE=2,
由△CEF∽△AEB知![]() =
=![]() ,即
,即![]() =
=![]() ,
,
则EF=![]() ,
,
∴S△CEF=![]() ×EF×CE=
×EF×CE=![]() ×2×
×2×![]() =
=![]() ;
;
综上所述,若△DFG是直角三角形,则△CEF的面积为15或![]() .
.

 科学实验活动册系列答案
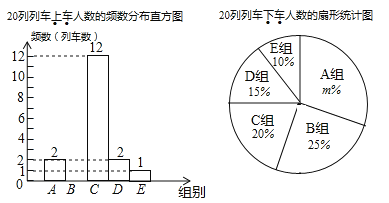
科学实验活动册系列答案【题目】根据重庆轨道集团提供的日客运量统计,2019年2月21日重庆轨道交通首次日客运量突破300万乘次,其中近期开通的重庆轨道交通环线日客运量为21.5万乘次.据了解,某工作日上午7点至9点轨道环线四公里站有20列列车进出站,每列车进出站时,将上车和下车的人数记录下来,各得到20个数据,并将数据进行整理,绘制成了如下两幅不完整统计图.(数据分组为:![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() )
)
I.上车人数在![]() 组的是:190,190,191,192,193,193,195,196,198,198,198,198;
组的是:190,190,191,192,193,193,195,196,198,198,198,198;
II.上车人数的平均数、中位数如下表:
平均数 | 中位数 | |
上车人数(人) | 194 | a |
根据以上信息,回答下列问题:
(1)请补全频数分布直方图;
(2)表中![]() ________,扇形统计图中
________,扇形统计图中![]() _________,扇形统计图中
_________,扇形统计图中![]() 组所在的圆心角度数为________度;
组所在的圆心角度数为________度;
(3)请利用平均数,估算一周内5个工作日的上午7点至9点重庆轨道环线四公里站的上车总人数.