题目内容
如图三角形ABC中,有一内接矩形EFGH,AD为BC边上的高,BC=10,AD=8,矩形面积为S,AD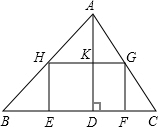 与HG交于K,设GF为x,HG为y.
与HG交于K,设GF为x,HG为y.(1)求y与x的函数关系式.
(2)当x取何值时,S有最大值,最大值是多少?
分析:(1)根据题意用含x的式子表示出AK,然后通过求证△AHG∽△ABC,根据对应边成比例,即可推出y与x的函数关系式;
(2)根据矩形的面积公式,则可推出S=xy,然后根据(1)的结论,即可表示出S关于x的二次函数式,根据二次函数的性质,即可推出x取何值时,S的值最大.
(2)根据矩形的面积公式,则可推出S=xy,然后根据(1)的结论,即可表示出S关于x的二次函数式,根据二次函数的性质,即可推出x取何值时,S的值最大.
解答:解:(1)∵矩形EFGH,AD⊥BC,
∴HG∥BC,
∴AK⊥HG,KD=GF,
∴△AHG∽△ABC,
∵BC=10,AD=8,GF为x,HG为y.
∴AK=8-x,
∵AK:AD=GH:BC,
∴
=
,
∴y=-
x+10;
(2)∵S矩形EFGH=GH•GF=xy=x•(-
x+10),
∴S=-
x2+10x,
∴x=-
=4,
∴当x=4时,S的值最大.
∴HG∥BC,
∴AK⊥HG,KD=GF,
∴△AHG∽△ABC,
∵BC=10,AD=8,GF为x,HG为y.
∴AK=8-x,
∵AK:AD=GH:BC,
∴
| 8-x |
| 8 |
| y |
| 10 |
∴y=-
| 5 |
| 4 |
(2)∵S矩形EFGH=GH•GF=xy=x•(-
| 5 |
| 4 |
∴S=-
| 5 |
| 4 |
∴x=-
| b |
| 2a |
∴当x=4时,S的值最大.
点评:本题主要考查相似三角形的判定和性质、矩形的性质、二次函数最值,关键是根据三角形相似,推出y关于x的函数表达式.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 按要求完成作图,并回答问题:如图三角形ABC中
按要求完成作图,并回答问题:如图三角形ABC中 17、如图三角形ABC中,∠B=∠C,EF∥BC,DF∥AB,则图中与∠B相等的角共有
17、如图三角形ABC中,∠B=∠C,EF∥BC,DF∥AB,则图中与∠B相等的角共有 按要求完成作图,并回答问题:如图三角形ABC中
按要求完成作图,并回答问题:如图三角形ABC中 与EF交于K,设GF为x,HG为y.
与EF交于K,设GF为x,HG为y.