题目内容
【题目】如图,长方形![]() 中,点
中,点![]() 沿着边按
沿着边按![]() .方向运动,开始以每秒
.方向运动,开始以每秒![]() 个单位匀速运动、
个单位匀速运动、![]() 秒后变为每秒
秒后变为每秒![]() 个单位匀速运动,
个单位匀速运动,![]() 秒后恢复原速匀速运动,在运动过程中,
秒后恢复原速匀速运动,在运动过程中,![]() 的面积
的面积![]() 与运动时间
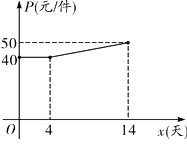
与运动时间![]() 的函数关系如图所示.
的函数关系如图所示.

(1)直接写出长方形的长和宽;
(2)求![]() ,
,![]() ,
,![]() 的值;
的值;
(3)当![]() 点在
点在![]() 边上时,直接写出
边上时,直接写出![]() 与
与![]() 的函数解析式.
的函数解析式.
【答案】(1)长方形的长为8,宽为4;(2)m=1,a=4,b=11;(3)S与t的函数解析式为![]() .
.
【解析】
(1)由图象可知:当6≤t≤8时,△ABP面积不变,由此可求得长方形的宽,再根据点P运动到点C时S△ABP=16,即可求出长方形的长;
(2)由图象知当t=a时,S△ABP=8=![]() S△ABP,可判断出此时点P的位置,即可求出a和m的值,再根据当t=b时,S△ABP=4,可求出AP的长,进而可得b的值;
S△ABP,可判断出此时点P的位置,即可求出a和m的值,再根据当t=b时,S△ABP=4,可求出AP的长,进而可得b的值;
(3)先判断![]() 与
与![]() 成一次函数关系,再用待定系数法求解即可.
成一次函数关系,再用待定系数法求解即可.
解:(1)从图象可知,当6≤t≤8时,△ABP面积不变,
∴6≤t≤8时,点P从点C运动到点D,且这时速度为每秒2个单位,
∴CD=2(8-6)=4,
∴AB=CD=4.
当t=6时(点P运动到点C),由图象知:S△ABP=16,
∴![]() ABBC=16,即
ABBC=16,即![]() ×4×BC=16.
×4×BC=16.
∴BC=8.
∴长方形的长为8,宽为4.
(2)当t=a时,S△ABP=8=![]() ×16,此时点P在BC的中点处,
×16,此时点P在BC的中点处,
∴PC=![]() BC=
BC=![]() ×8=4,
×8=4,
∴2(6-a)=4,
∴a=4.
∵BP=PC=4,
∴m=![]() =
=![]() =1.
=1.
当t=b时,S△ABP=![]() ABAP=4,
ABAP=4,
∴![]() ×4×AP=4,AP=2.
×4×AP=4,AP=2.
∴b=13-2=11.
故m=1,a=4,b=11.
(3)当8≤t≤11时,S关于t的函数图象是过点(8,16),(11,4)的一条线段,
可设S=kt+b,∴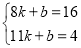 ,解得
,解得![]() ,∴S=-4t+48(8≤t≤11).
,∴S=-4t+48(8≤t≤11).
同理可求得当11<t≤13时,S关于t的函数解析式为S=-2t+26(11<t≤13).
∴S与t的函数解析式为![]() .
.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案