题目内容
 15、如图,已知梯形ABCD中,AD∥BC,BD是对角线.添加下列条件之一:
15、如图,已知梯形ABCD中,AD∥BC,BD是对角线.添加下列条件之一:①AB=DC;②BD平分∠ABC;③∠ABC=∠C;④∠A+∠C=180°,能推得梯形ABCD是等腰梯形的是
①③④
(填编号).分析:①根据等腰梯形的定义可以判定等腰梯形;
②只能得到AD=AB,但不能判定等腰梯形;
③根据同一底边上的两底角相等的梯形是等腰梯形进行判定;
④根据此条件可以得到同一底边上的两底角相等.
②只能得到AD=AB,但不能判定等腰梯形;
③根据同一底边上的两底角相等的梯形是等腰梯形进行判定;
④根据此条件可以得到同一底边上的两底角相等.
解答:解:∵梯形ABCD中,AD∥BC,AB=DC,
∴梯形ABCD是等腰梯形,故①正确;
②既不能得到两同一底边上的两底角相等,也不能得到两腰相等,
故②错误;
③∵梯形ABCD中,AD∥BC,∠ABC=∠C,
∴根据同一底边上的两底角相等可以判定等腰梯形,
∴③正确;
④∵AD∥BC,
∴∠A=∠ABC,
∵∠A+∠C=180°,
∴∠ABC=∠C,
∴梯形ABCD是等腰梯形,故④正确.
故答案为:①③④.
∴梯形ABCD是等腰梯形,故①正确;
②既不能得到两同一底边上的两底角相等,也不能得到两腰相等,
故②错误;
③∵梯形ABCD中,AD∥BC,∠ABC=∠C,
∴根据同一底边上的两底角相等可以判定等腰梯形,
∴③正确;
④∵AD∥BC,
∴∠A=∠ABC,
∵∠A+∠C=180°,
∴∠ABC=∠C,
∴梯形ABCD是等腰梯形,故④正确.
故答案为:①③④.
点评:本题考查了等腰梯形的判定,解题的关键是熟悉等腰梯形的判定方法.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
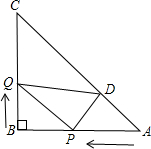 点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s.
点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s. (2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为
(2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为