题目内容
观察下面的各个等式:
=
-1,
=
-
,
=
-
,
=
-
,…从上述等式中找出规律,并用这一规律计算:(
+
+
+…+
)(
+1)=
| 1 | ||
|
| 2 |
| 1 | ||||
|
| 3 |
| 2 |
| 1 | ||||
|
| 4 |
| 3 |
| 1 | ||||
|
| 5 |
| 4 |
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2004 |
2003
2003
.分析:先将第一个括号内的各式分母有理化,此时发现除第二项和倒数第二项外,其他各项的和为0,由此可求出第一个括号内代数式的值,进而可根据平方差公式求出整个代数式的值.
解答:解:从等式
=
-1,
=
-
,
=
-
,
=
-
,…中找出规律:
=
-
(n是整数,且n≥1).
则(
+
+
+…+
)(
+1)
=(
-1+
-
+…+
-
)(
+1)
=(
-1)(
+1)
=2004-1
=2003
故答案是:2003.
| 1 | ||
|
| 2 |
| 1 | ||||
|
| 3 |
| 2 |
| 1 | ||||
|
| 4 |
| 3 |
| 1 | ||||
|
| 5 |
| 4 |
| 1 | ||||
|
| n+1 |
| n |
则(
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2004 |
=(
| 2 |
| 3 |
| 2 |
| 2004 |
| 2003 |
| 2004 |
=(
| 2004 |
| 2004 |
=2004-1
=2003
故答案是:2003.
点评:此题考查的是二次根式的混合运算,能够发现式子中的规律是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =
= -1,
-1,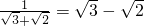 ,
,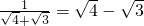 ,
,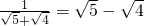 ,…从上述等式中找出规律,并用这一规律计算:(
,…从上述等式中找出规律,并用这一规律计算:( )(
)( +1)=________.
+1)=________.