Question

【题目】在如图的正方形网格中，每一个小正方形的边长为1．格点三角形ABC（顶点是网格线交点的三角形）的顶点A、C的坐标分别是（﹣4，6），（﹣1，4）．

（1）请在图中的网格平面内建立平面直角坐标系；

（2）请画出△ABC关于x轴对称的△A1B1C1；

（3）△ABC　 　直角三角形（填“是”或“不是”）；

（4）请在y轴上画一点P，使△PB1C的周长最小，并写出点P的坐标．

Answer 1

【答案】（1）平面直角坐标系见详解，（2）见详解，（3）不是，（4）P点见详解作图，.

【解析】

(1)根据A点坐标建立平面直角坐标系即可,

(2)分别作出各点关于x轴的对称点，再顺次连接即可,

(3)利用勾股定理分别求出AB,BC,AC的长，即可证明是否满足勾股定理，

(4) 作出点B关于y轴的对称点B2，连接B2交y轴于点P，则P点即为所求．

解：（1）平面直角坐标系如图.

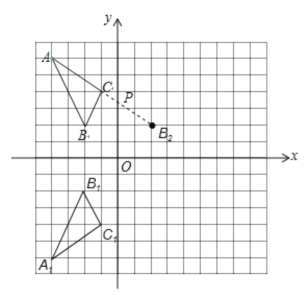
（2）△ABC关于x轴对称的△A1B1C1如上图.

（3）A、C的坐标分别是（﹣4，6），（﹣1，4）,且每一个小正方形的边长为1，利用勾股定理求得有

有即

故△ABC不是直角三角形.

（4）)作点B关于y轴的对称点，连接A交y轴于点P，则点P即为所求.

设直线A的解析式为y=kx＋b(k≠0),

∵A(-4，6)， (2，2)，

∴解得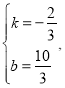

∴直线A的解析式为：

∴当x=0时，y=，

∴P点的坐标为 .