题目内容
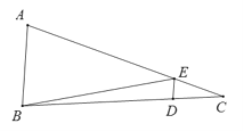
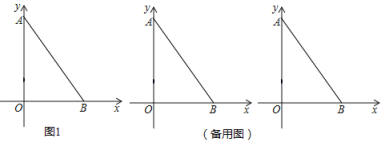
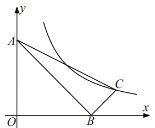
【题目】如图,已知在平面直角坐标系中,Rt△ABC的顶点A、B的坐标分别是(0,3)、(3,0),∠ABC=90°AC=![]() ,则函数
,则函数![]() 的图象经过点C,则
的图象经过点C,则![]() 的值为( )
的值为( )
A.3B.4C.6D.9
【答案】B
【解析】
根据A、C的坐标分别是(0,3)、(3、0)可知OA=OB=3,进而可求出AB,由勾股定理可求BC,通过作垂线构造等腰直角三角形,求出点C的坐标,再求出k的值.
解:过点C作CD⊥x轴,垂足为D,

∵A、B的坐标分别是(0,3)、(3,0),∠AOB=90°,
∴OA=OB=3,∠OBA=45°,
∴AB=![]() ,
,
∵∠ABC=90°,AC=![]() ,
,
∴BC=![]() .
.
∵CD⊥x轴,
∴∠CDB=90°,∠CBD=![]() ,
,
∴△BCD是等腰直角三角形,
则设BC=CD=x,
∴![]() ,
,
解得:![]() ;
;
∴点C的坐标为:(4,1),
∵点C在反比例函数![]() 上,
上,
∴![]() ;
;
故选择:B.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标x纵坐标y的对应值如下表
上部分点的横坐标x纵坐标y的对应值如下表
x |
|
|
| 0 | 1 | 2 |
|
y |
| 0 |
|
| 0 | 8 |
|
![]() 写出该抛物线的对称轴及当
写出该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
![]() 求出抛物线
求出抛物线![]() 的解析式,并在平面直角坐标系中画出该抛物线的图象;
的解析式,并在平面直角坐标系中画出该抛物线的图象;
(3)结合图象回答:
①不等式![]() 的解集是___________________;
的解集是___________________;
②当![]() 时,y的取值范围是__________________.
时,y的取值范围是__________________.