题目内容
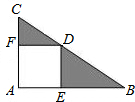 如图,Rt△ABC中,E、D、F分别在AB、BC、AC上,且四边形AEDF是正方形.已知CD=8,BD=12,则阴影部分的面积为
如图,Rt△ABC中,E、D、F分别在AB、BC、AC上,且四边形AEDF是正方形.已知CD=8,BD=12,则阴影部分的面积为分析:设正方形AEDF的边长为a,由四边形AEDF为正方形,∠BAC=90°,得DF∥AB,得到△CDF∽△DBE,根据相似三角形的对应边成比例,即可求得CF与BF的值,在Rt△BDE中,利用勾股定理可得到a2,再利用三角形的面积公式得S阴影部分=
•CF•DF+
•DE•BE,代入计算即可得到阴影部分的面积.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设正方形AEDF的边长为a,
∵四边形AEDF为正方形,∠BAC=90°,
∴DF∥AB,
∴∠CDF=∠B,
∴△CDF∽△DBE,
∴
=
=
,
∴BE=
,CF=
,
在Rt△BDE中,BD2=BE2+DE2,即122=a2+(
)2,
解得a2=
,
∴S阴影部分=
•CF•DF+
•DE•BE=
(
+
)=
×
×
=48.
故答案为48.
∵四边形AEDF为正方形,∠BAC=90°,
∴DF∥AB,
∴∠CDF=∠B,
∴△CDF∽△DBE,
∴
| 8 |
| 12 |
| a |
| BE |
| CF |
| a |
∴BE=
| 3a |
| 2 |
| 2a |
| 3 |
在Rt△BDE中,BD2=BE2+DE2,即122=a2+(
| 3a |
| 2 |
解得a2=
| 576 |
| 13 |
∴S阴影部分=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3a2 |
| 2 |
| 2a2 |
| 3 |
| 1 |
| 2 |
| 13 |
| 6 |
| 576 |
| 13 |
故答案为48.
点评:本题考查了三角形相似的判定与性质,勾股定理以及三角形的面积公式.此题难度较大,解题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.