Question

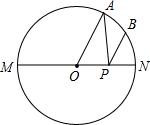如图所示，已知点A是半圆上的三等分点，B是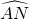的中点，P是直径MN上一动点，⊙O的半径为1．请问：P在MN上什么位置时，AP+BP的值最小？并给出AP+BP的最小值．

Answer 1

解：P位于A′B与MN的交点处，AP+BP的值最小；
作A关于MN的对称点A′，根据圆的对称性，则A′必在圆上，
连接BA′交MN于P，连接PA，则PA+PB最小，此时PA+PB=PA′+PB=A′B，
连接OA、OA′、OB，
∵=，
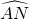∴∠AON=∠A′ON=60°．
∵=，
∴∠BON=∠AON=30°．
∴∠A′OB=90°．
∴A′B===．
即AP+BP的最小值是．
分析：通过作辅助线，根据“两点之间线段最短”可将AP+BP的最小值转化为求直角三角形的斜边长．
点评：此题主要考查了轴对称最短路线问题以及勾股定理和垂径定理等知识，根据已知得出P点位置是解题关键．