题目内容

求最大的正整数n，使得n3+100能被n+10整除．
分析：根据题意列出算式，变形后得到900能整除n+10，即可确定出最大的正整数n的值．
解答：解：要使（n3+100）÷（n+10）=
n3+100
n+10
=
(n+10)(n-10)2-900
n+10
=（n-10）2-
900
n+10
为整数，
必须900能整除n+10，
则n的最大值为890．
点评：此题考查了整式的除法，熟练掌握单项式除单项式法则是解本题的关键．
练习册系列答案
相关题目
（1）定义f(x)=
1
3x2+2x+1
+
3x2-1
+
3x2-2x+1
，求f（1）+f（3）+…+f（2k-1）+f（999）的值；
（2）设x、y都是正整数，且使
x-116
+
x+100
=y，求y的最大值．
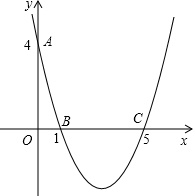精英家教网如图，在平面直角坐标系xoy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线对称轴l与x轴相交于点M．
（1）求抛物线的解析式和对称轴；
（2）点P在抛物线上，且以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数，请你直接写出点P的坐标；
（3）连接AC．探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求出点N的坐标；若不存在，请你说明理由．
（2012•辽阳）某商店经营儿童益智玩具，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件玩具售价不能高于40元．设每件玩具的销售单价上涨了x元时（x为正整数），月销售利润为y元．
（1）求y与x的函数关系式并直接写出自变量x的取值范围．
（2）每件玩具的售价定为多少元时，月销售利润恰为2520元？
（3）每件玩具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
某商店经营一种文化衫，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件文化衫售价不能高于40元．设每件文化衫的销售单价上涨了x元时（x为正整数），月销售利润为y元．
（1）求y与x的函数关系式并直接写出自变量x的取值范围．
（2）每件文化衫的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
（2012•黔西南州）如图，在平面直角坐标系xOy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线的对称轴l与x轴相交于点M．
（1）求抛物线对应的函数解析式和对称轴；
（2）设点P为抛物线（x＞5）上的一点，若以A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数，请你直接写出点P的坐标；
（3）连接AC，探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求出点N的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网