题目内容
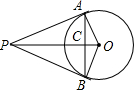
如图，PA，PB为⊙O切线，∠BOC=42°，则∠P=________．
42°
分析：由PA，PB为⊙O切线，可得出OA⊥AP，OB⊥BP；进而由角度关系：∠P=180°-∠AOB，∠AOB=180°-∠BOC，可得出∠P的度数．
解答：∵PA，PB为⊙O切线，
∴OA⊥AP，OB⊥BP，
∴∠P=180°-∠AOB；
∵∠AOB=180°-∠BOC，
∴∠P=∠BOC=42°，
故此题应该填42°．
点评：本题考查了切线的性质．
分析：由PA，PB为⊙O切线，可得出OA⊥AP，OB⊥BP；进而由角度关系：∠P=180°-∠AOB，∠AOB=180°-∠BOC，可得出∠P的度数．
解答：∵PA，PB为⊙O切线，
∴OA⊥AP，OB⊥BP，
∴∠P=180°-∠AOB；
∵∠AOB=180°-∠BOC，
∴∠P=∠BOC=42°，
故此题应该填42°．
点评：本题考查了切线的性质．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
如图，PA，PB为⊙O的切线，A，B分别为切点，∠APB=60°，点P到圆心O的距离OP=2，则⊙O的半径为（ ）A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
（1）如图，PA、PB为⊙O的两条切线，点A、B分别为切点，OP与弦AB交于点C．①写出三对全等的三角形；②选择其中一对加以证明；
如图，PA、PB为⊙O的切线，AC为经过切点A的直径，求证：BC∥PO．
如图，PA、PB为⊙O的切线，AC为经过切点A的直径，求证：BC∥PO．
