题目内容
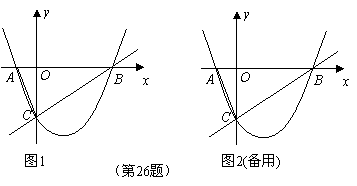
如图1,已知:抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,经过
,经过![]() 两点的直线是
两点的直线是![]() ,连结
,连结![]() .
.
(1)![]() 两点坐标分别为
两点坐标分别为![]() (_____,_____)、
(_____,_____)、![]() (_____,_____),抛物线的函数关系式为______________;
(_____,_____),抛物线的函数关系式为______________;
(2)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)若![]() 内部能否截出面积最大的矩形
内部能否截出面积最大的矩形![]() (顶点
(顶点![]() 在
在![]() 各边上)?若能,求出在
各边上)?若能,求出在![]() 边上的矩形顶点的坐标;若不能,请说明理由.(本题共11分)
边上的矩形顶点的坐标;若不能,请说明理由.(本题共11分)
答案:解:(1)![]() (4,0),
(4,0),![]() .
.
![]() .
.
(2)![]() 是直角三角形.
是直角三角形.
证明:令![]() ,则
,则![]() .
.
![]() .
.
![]() .
.
解法一:![]() .
.
![]() .
.
![]() 是直角三角形.
是直角三角形.
解法二:![]()
![]() .
.
![]() .
.
![]() ,
,
![]() .即
.即![]() .
.
![]() 是直角三角形.
是直角三角形.

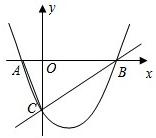
(3)能.![]() 当矩形两个顶点在
当矩形两个顶点在![]() 上时,如图1,
上时,如图1,![]() 交
交![]() 于
于![]() .
.
![]() ,
,
![]() .
.
![]() .
.
解法一:设![]() ,则
,则![]() ,
,![]() ,
,
![]() .
.
![]() =
=![]() .
.
当![]() 时,
时,![]() 最大.
最大.
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,![]() .
.
解法二:设![]() ,则
,则![]() .
.

![]() .
.
![]() 当
当![]() 时,
时,![]() 最大.
最大.
![]() .
.
![]() ,
,
![]()
![]() ,
,![]() .
.
![]() 当矩形一个顶点在
当矩形一个顶点在![]() 上时,
上时,![]() 与
与![]() 重合,如图2,
重合,如图2,
![]() ,
,
![]() .
.
![]() .
.
解法一:设![]() ,
,![]() ,
,
![]() .
.
![]()
![]() =
=![]() .
.
当![]() 时,
时,![]() 最大.
最大.
![]() ,
,![]() .
.![]()
![]()
解法二:设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() .
.
![]() =
=
![]() 当
当![]() 时,
时,![]() 最大,
最大,
![]() .
.![]() .
.![]()
![]()
![]()
综上所述:当矩形两个顶点在![]() 上时,坐标分别为
上时,坐标分别为![]() ,(2, 0);
,(2, 0);
当矩形一个顶点在![]() 上时,坐标为
上时,坐标为![]() .
.

练习册系列答案
相关题目
 如图1,已知:抛物线
如图1,已知:抛物线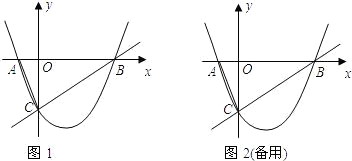

 与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是
与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是 ,连结AC.
,连结AC.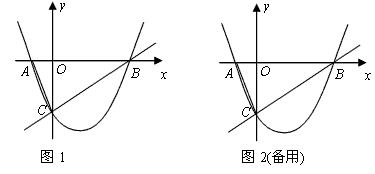
 的顶点坐标是
的顶点坐标是 ]
]