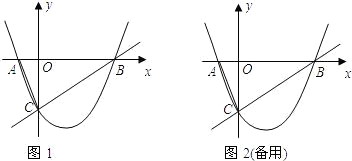
��Ŀ����
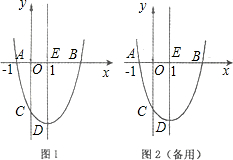
��ͼ1����֪��������y=| 1 |
| 2 |
| 1 |
| 2 |
��1��B��C��������ֱ�ΪB��
��2���жϡ�ABC����״����˵�����ɣ�
��3������ABC�ڲ��ܷ�س�������ľ���DEFC������D��E��F��G�ڡ�ABC�����ϣ������ܣ������AB���ϵľ��ζ�������ꣻ�����ܣ���˵�����ɣ�
��������1����x=0�Լ�y=0����y=
x-2�ó�B��C�����꣮�����������������߿ɵú�����ϵʽ��
��2����֪AB��AC��BC��ֵ�����ݷ����ɶ�����֤����ABC��ֱ�������Σ�
��3��֤����CGF�ס�CAB�������߶α�����й��߶ε�ֵ�����S����DEFG�����ֵ���ٸ��ݡ�ADG�ס�AOC���߶α���⣮
| 1 |
| 2 |
��2����֪AB��AC��BC��ֵ�����ݷ����ɶ�����֤����ABC��ֱ�������Σ�
��3��֤����CGF�ס�CAB�������߶α�����й��߶ε�ֵ�����S����DEFG�����ֵ���ٸ��ݡ�ADG�ס�AOC���߶α���⣮
����⣺��1����x=0��y=-2��
��y=0����y=
x-2��x=4��
��B��C������ֱ�Ϊ��
B��4��0����C��0��-2������2�֣�
y=
x2-
x-2����4�֣�
��2����ABC��ֱ�������Σ���5�֣�
֤������y=0����
x2-
x-2=0��
��x1=-1��x2=4��
��A��-1��0������6�֣�
�ⷨһ����AB=5��AC=
��BC=2
����7�֣�
��AC2+BC2=5+20=25=AB2��
���ABC��ֱ�������Σ���8�֣�
�ⷨ������AO=1��CO=2��BO=4��
��
=
=
�ߡ�AOC=��COB=90�㣬
���AOC�ס�COB����7�֣�
���ACO=��CBO��
�ߡ�CBO+��BCO=90�㣬
���ACO+��BCO=90�ȣ�
����ACB=90�ȣ�
���ABC��ֱ�������Σ���8�֣�
��3���ܣ��ٵ���������������AB��ʱ����ͼ1��CO��GF��H��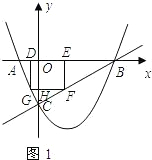
��GF��AB��
���CGF�ס�CAB��
��
=
����9�֣�
�ⷨһ����GF=x����DE=x��
CH=
x��DG=OH=OC-CH=2-
x��
��S����DEFG=x•��2-
x��=-
x2+2x=-
��x-
��2+
����10�֣�
��x=
ʱ��S���
��DE=
��DG=1��
�ߡ�ADG�ס�AOC��
��
=
��
��AD=
��
��OD=
��OE=2��
��D��-
��0����E��2��0������11�֣�
�ⷨ������DG=x����DE=GF=
��
��S����DEFG=x•
=-
x2+5x=-
��x-1��2+
����10�֣�
�൱x=1ʱ��S���
��DG=1��DE=
��
�ߡ�ADG�ס�AOC��
��
=
��
��AD=
��
��OD=
��OE=2��
��D��-
��0����E��2��0������11�֣�
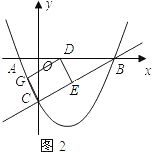
�ڵ�����һ��������AB��ʱ��F��C�غϣ���ͼ2��
��DG��BC��
���AGD�ס�ACB��
��
=
��
�ⷨһ����GD=x��
��AC=
��BC=2
��
��GF=AC-AG=
-
��
��S����DEFG=x•��
-
��=-
x2+
x
=-
��x-
��2+
����12�֣�
��x=
ʱ��S���GD=
��AG=
��
��AD=
=
��
��OD=
��D��
��0����13�֣�
�ⷨ������DE=x��
��AC=
��BC=2
��
��GC=x��AG=
-x��
��GD=2
-2x��
��S����DEFG=x•��2
-2x��=-2x2+2
x=-2��x-
��2+
��12�֣�
�൱x=
ʱ��S���
��GD=
��AG=
��
��AD=
=
��
��OD=
��D��
��0����13�֣�
��������������������������AB��ʱ������ֱ�Ϊ��-
��0������2��0��
������һ��������AB��ʱ������Ϊ��
��0������14�֣�
��y=0����y=
| 1 |
| 2 |
��B��C������ֱ�Ϊ��
B��4��0����C��0��-2������2�֣�
y=
| 1 |
| 2 |
| 3 |
| 2 |
��2����ABC��ֱ�������Σ���5�֣�
֤������y=0����
| 1 |
| 2 |
| 3 |
| 2 |
��x1=-1��x2=4��
��A��-1��0������6�֣�
�ⷨһ����AB=5��AC=
| 5 |
| 5 |
��AC2+BC2=5+20=25=AB2��
���ABC��ֱ�������Σ���8�֣�
�ⷨ������AO=1��CO=2��BO=4��
��
| CO |
| BO |
| AO |
| OC |
| 1 |
| 2 |
�ߡ�AOC=��COB=90�㣬
���AOC�ס�COB����7�֣�
���ACO=��CBO��
�ߡ�CBO+��BCO=90�㣬
���ACO+��BCO=90�ȣ�
����ACB=90�ȣ�
���ABC��ֱ�������Σ���8�֣�
��3���ܣ��ٵ���������������AB��ʱ����ͼ1��CO��GF��H��

��GF��AB��
���CGF�ס�CAB��
��
| GF |
| AB |
| CH |
| CO |
�ⷨһ����GF=x����DE=x��
CH=
| 2 |
| 5 |
| 2 |
| 5 |
��S����DEFG=x•��2-
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 2 |
��x=
| 5 |
| 2 |
��DE=
| 5 |
| 2 |
�ߡ�ADG�ס�AOC��
��
| AD |
| AO |
| DG |
| OC |
��AD=
| 1 |
| 2 |
��OD=
| 1 |
| 2 |
��D��-
| 1 |
| 2 |
�ⷨ������DG=x����DE=GF=
| 10-5x |
| 2 |
��S����DEFG=x•
| 10-5x |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
�൱x=1ʱ��S���
��DG=1��DE=
| 5 |
| 2 |
�ߡ�ADG�ס�AOC��
��
| AD |
| AO |
| DG |
| OC |
��AD=
| 1 |
| 2 |
��OD=
| 1 |
| 2 |
��D��-
| 1 |
| 2 |
�ڵ�����һ��������AB��ʱ��F��C�غϣ���ͼ2��
��DG��BC��
���AGD�ס�ACB��
��
| GD |
| BC |
| AG |
| AF |

�ⷨһ����GD=x��
��AC=
| 5 |
| 5 |
��GF=AC-AG=
| 5 |
| x |
| 2 |
��S����DEFG=x•��
| 5 |
| x |
| 2 |
| 1 |
| 2 |
| 5 |
=-
| 1 |
| 2 |
| 5 |
| 5 |
| 2 |
��x=
| 5 |
| 5 |
| ||
| 2 |
��AD=
| AG2+GD2 |
| 5 |
| 2 |
��OD=
| 3 |
| 2 |
| 3 |
| 2 |
�ⷨ������DE=x��

��AC=
| 5 |
| 5 |
��GC=x��AG=
| 5 |
��GD=2
| 5 |
��S����DEFG=x•��2
| 5 |
| 5 |
| ||
| 2 |
| 5 |
| 2 |
�൱x=
| ||
| 2 |
��GD=
| 5 |
| ||
| 2 |
��AD=
| AG2+GD2 |
| 5 |
| 2 |
��OD=
| 3 |
| 2 |
��D��
| 3 |
| 2 |
��������������������������AB��ʱ������ֱ�Ϊ��-
| 1 |
| 2 |
������һ��������AB��ʱ������Ϊ��
| 3 |
| 2 |
���������⿼����Ƕ��κ������ۺ������Լ����������Ƶ��ж�������Ҫѧ��������ö��κ��������֪ʶ��

��ϰ��ϵ�д�
 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
�����Ŀ
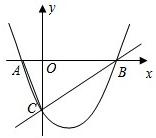 ��ͼ1����֪��������
��ͼ1����֪��������
 ��x�ύ��A��B���㣬��y�ύ�ڵ�C������B��C�����ֱ����
��x�ύ��A��B���㣬��y�ύ�ڵ�C������B��C�����ֱ���� ������AC��
������AC��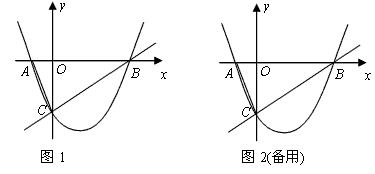
 �Ķ���������
�Ķ��������� ]
]