题目内容
如图,四边形ABCD中,AB⊥BC,∠A+∠B =160°,∠D=4∠C,求四边形ABCD各内角的度数.
=160°,∠D=4∠C,求四边形ABCD各内角的度数.

【考点】多边形内角与外角.
【分析】根据垂直定义可得∠B=90°,根据∠A和∠B的关系可得∠A的度数,再根据四边形内角和定理可得∠C+∠D=200°,再结合∠D=4∠C可得答案.
【解答】解:∵AB⊥BC,
∴∠B=90°,
∵∠A+∠B=160°,
∴∠A=70°,
∵∠A+∠B+∠C+∠D=360°,
∴∠C+∠D=200°,
∵∠D=4∠C,
∴∠C=40°,
∴∠D=160°.
【点评】此题主要考查了多边形内角,关键是掌握四边形内角和为360°.

练习册系列答案
相关题目




 C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.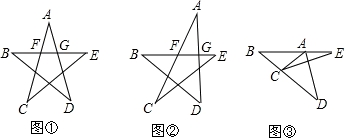

 ,求该直线的函数关系式.
,求该直线的函数关系式. 的绝对值的相反数是_______.
的绝对值的相反数是_______.