题目内容
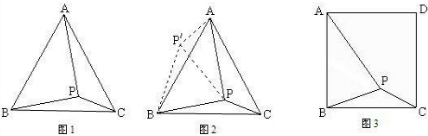
(1)如图1,在等边三角形ABCD中,M是BC上任意一点,以M为顶点,AM为一边,作∠AMN=∠B.在MN上截取MP=AM,连接CP,求∠MCP的度数.
(2)如图2,在等边三角形ABC中,M是BC上任意一点,以M为顶点,AM为一边,作∠AMN=∠B.在MN上截取MP=AM,连接CP,求∠MCP的度数.
(3)若将正方形或等边三角形变为正五边形,其他条件不变,如图3,则∠MCP=
(4)若将正方形或等边三角形变为正n边形,其他条件不变,则∠MCP=

(2)如图2,在等边三角形ABC中,M是BC上任意一点,以M为顶点,AM为一边,作∠AMN=∠B.在MN上截取MP=AM,连接CP,求∠MCP的度数.
(3)若将正方形或等边三角形变为正五边形,其他条件不变,如图3,则∠MCP=
144°
144°
.(4)若将正方形或等边三角形变为正n边形,其他条件不变,则∠MCP=
(180-
)°
| 180 |
| n |
(180-
)°
(用含n的代数式表示).| 180 |
| n |

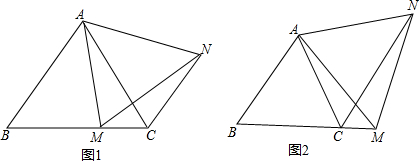
分析:(1)在BQ上取一点W,使∠PWM=∠B,证△BAM≌△WMP,推出AB=BC=MW,BM=PW,推出PW=WC=BM,求出∠PCW,即可求出答案.
(2)在BQ上取一点W,使∠PWM=∠B,证△BAM≌△WMP,推出AB=BC=MW,BM=PW,推出PW=WC=BM,求出∠PCW,即可求出答案.
(3)在BQ上取一点W,使∠PWM=∠B,证△BAM≌△WMP,推出AB=BC=MW,BM=PW,推出PW=WC=BM,求出∠PCW,即可求出答案.
(4)在BQ上取一点W,使∠PWM=∠B,证△BAM≌△WMP,推出AB=BC=MW,BM=PW,推出PW=WC=BM,求出∠PCW,即可求出答案.
(2)在BQ上取一点W,使∠PWM=∠B,证△BAM≌△WMP,推出AB=BC=MW,BM=PW,推出PW=WC=BM,求出∠PCW,即可求出答案.
(3)在BQ上取一点W,使∠PWM=∠B,证△BAM≌△WMP,推出AB=BC=MW,BM=PW,推出PW=WC=BM,求出∠PCW,即可求出答案.
(4)在BQ上取一点W,使∠PWM=∠B,证△BAM≌△WMP,推出AB=BC=MW,BM=PW,推出PW=WC=BM,求出∠PCW,即可求出答案.
解答: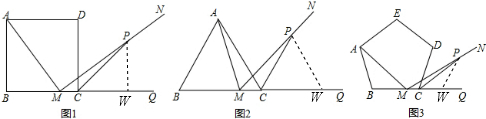
解:(1)在BQ上取一点W,使∠PWM=∠B,如图1,
∵四边形ABCD是正方形,∠AMP=∠B,
∴AB=BC,∠B=∠PWC=∠AMP=90°,
∴∠BAM+∠AMB=∠AMB+∠PMW=180°-90°=90°,
∴∠BAM=∠WMP,
在△ABM和△MWP中
∴△ABM≌△MWP(AAS),
∴BM=PW,AB=MW=BC,
∴BC-BM=MW-CM,
∴BM=CW=PW,
∵∠PWC=90°,
∴∠PCW=∠WPC=45°,
∴∠MCP=180°-∠PCW=180°-45°=135°;
(2)在BQ上取一点W,使∠PWM=∠B,如图2,
∵△ABC是等边三角形,∠AMP=∠B,
∴AB=BC,∠B=∠PWM=∠AMP=60°,
∴∠BAM+∠AMB=∠AMB+∠PMW=180°-60°=120°,
∴∠BAM=∠WMP,
在△ABM和△MWP中
∴△ABM≌△MWP(AAS),
∴BM=PW,AB=MW=BC,
∴BC-BM=MW-CM,
∴BM=CW=PW,
∵∠PWC=60°,
∴∠PCW=∠WPC=
(180°-60°)=60°,
∴∠MCP=180°-∠PCW=180°-60°=120°;
(3)在BQ上取一点W,使∠PWM=∠B,如图3,
∵五边形ABCDE是正五方形,∠AMP=∠B=
=108°,
∴AB=BC,∠B=∠PWC=∠AMP=108°,
∴∠BAM+∠AMB=∠AMB+∠PMW=180°-108°=72°,
∴∠BAM=∠WMP,
在△ABM和△MWP中,
,
∴△ABM≌△MWP(AAS),
∴BM=PW,AB=MW=BC,
∴BC-BM=MW-CM,
∴BM=CW=PW,
∵∠PWC=108°,
∴∠PCW=∠WPC=
(180°-108°)=36°,
∴∠MCP=180°-∠PCW=180°-36°=144°,
故答案为:144°;
(4)∵正n边形ABCDE…是正n方形,∠AMP=∠B=
,
∴AB=BC,∠B=∠PWC=∠AMP=
,
∴∠BAM+∠AMB=∠AMB+∠PMW=180°-∠B,
∴∠BAM=∠WMP,
在△ABM和△MWP中,
,
∴△ABM≌△MWP(AAS),
∴BM=PW,AB=MW=BC,
∴BC-BM=MW-CM,
∴BM=CW=PW,
∵∠PWC=
,
∴∠PCW=∠WPC=
[180°-
],
∴∠MCP=180°-∠PCW=180°-
[180°-
]=90°+
=(180-
)°,
故答案为:(180-
)°.

解:(1)在BQ上取一点W,使∠PWM=∠B,如图1,
∵四边形ABCD是正方形,∠AMP=∠B,
∴AB=BC,∠B=∠PWC=∠AMP=90°,
∴∠BAM+∠AMB=∠AMB+∠PMW=180°-90°=90°,
∴∠BAM=∠WMP,
在△ABM和△MWP中
|
∴△ABM≌△MWP(AAS),
∴BM=PW,AB=MW=BC,
∴BC-BM=MW-CM,
∴BM=CW=PW,
∵∠PWC=90°,
∴∠PCW=∠WPC=45°,
∴∠MCP=180°-∠PCW=180°-45°=135°;
(2)在BQ上取一点W,使∠PWM=∠B,如图2,
∵△ABC是等边三角形,∠AMP=∠B,
∴AB=BC,∠B=∠PWM=∠AMP=60°,
∴∠BAM+∠AMB=∠AMB+∠PMW=180°-60°=120°,
∴∠BAM=∠WMP,
在△ABM和△MWP中
|
∴△ABM≌△MWP(AAS),
∴BM=PW,AB=MW=BC,
∴BC-BM=MW-CM,
∴BM=CW=PW,
∵∠PWC=60°,
∴∠PCW=∠WPC=
| 1 |
| 2 |
∴∠MCP=180°-∠PCW=180°-60°=120°;
(3)在BQ上取一点W,使∠PWM=∠B,如图3,
∵五边形ABCDE是正五方形,∠AMP=∠B=
| (5-2)×180° |
| 5 |
∴AB=BC,∠B=∠PWC=∠AMP=108°,
∴∠BAM+∠AMB=∠AMB+∠PMW=180°-108°=72°,
∴∠BAM=∠WMP,
在△ABM和△MWP中,
|
∴△ABM≌△MWP(AAS),
∴BM=PW,AB=MW=BC,
∴BC-BM=MW-CM,
∴BM=CW=PW,
∵∠PWC=108°,
∴∠PCW=∠WPC=
| 1 |
| 2 |
∴∠MCP=180°-∠PCW=180°-36°=144°,
故答案为:144°;
(4)∵正n边形ABCDE…是正n方形,∠AMP=∠B=
| (n-2)×180° |
| n |
∴AB=BC,∠B=∠PWC=∠AMP=
| (n-2)×180° |
| n |
∴∠BAM+∠AMB=∠AMB+∠PMW=180°-∠B,
∴∠BAM=∠WMP,
在△ABM和△MWP中,
|
∴△ABM≌△MWP(AAS),
∴BM=PW,AB=MW=BC,
∴BC-BM=MW-CM,
∴BM=CW=PW,
∵∠PWC=
| (n-2)×180° |
| n |
∴∠PCW=∠WPC=
| 1 |
| 2 |
| (n-2)×180° |
| n |
∴∠MCP=180°-∠PCW=180°-
| 1 |
| 2 |
| (n-2)×180° |
| n |
| (n-2)×90° |
| n |
| 180 |
| n |
故答案为:(180-
| 180 |
| n |
点评:本题考查了全等三角形的性质和判定,正n边形的性质,等腰三角形的性质,三角形的内角和定理的应用,题目具有一定的代表性,证明过程类似.

练习册系列答案
相关题目