题目内容
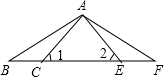 已知命题:如图,点B、C、E、F在同一直线上,若AB=AF,∠1=∠2,则△ABE≌△AFC.
已知命题:如图,点B、C、E、F在同一直线上,若AB=AF,∠1=∠2,则△ABE≌△AFC.请判断这个命题是真命题还是假命题,如果是真命题,请给予证明;如果是假命题,请添加一个条件使它成为真命题,并加以证明.
考点:全等三角形的判定,命题与定理
专题:常规题型
分析:先根据等腰三角形的性质,由AB=AF得到∠B=∠F,于是可根据“AAS”判定△ABE≌△AFC.
解答:解:这个命题是真命题.
证明如下:
∵AB=AF,
∴∠B=∠F,
在△ABE和△AFC中,
,
∴△ABE≌△AFC(AAS).
证明如下:
∵AB=AF,
∴∠B=∠F,
在△ABE和△AFC中,
|
∴△ABE≌△AFC(AAS).
点评:本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
某市民政部门:五一期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票2元),在这些彩票中,设置如下奖项:
如果花2元钱购买1张彩票,那么所得奖金不少于50元的概率是( )
| 奖金(元) | 1 000 | 500 | 100 | 50 | 10 | 2 |
| 数量(个) | 10 | 40 | 150 | 400 | 1 000 | 10 000 |
A、
| ||
B、
| ||
C、
| ||
D、
|
整式2x2y-xy+6的项数和次数分别是( )
| A、2,3 | B、2,2 |
| C、3,2 | D、3,3 |
 在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于点D,求∠DBC的度数.
在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于点D,求∠DBC的度数.