题目内容
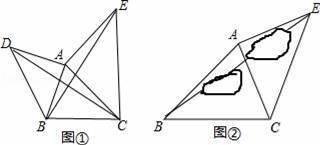
探索:如图①,以△ABC的边AB、AC为直角边,A为直角顶点,向外作等腰直角△ABD和等腰直角△ACE,连结BE、CD,试确定BE与CD有怎样数量关系,并说明理由.
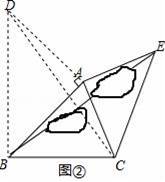
应用:如图②,要测量池塘两岸B、E两地之间的距离,已知测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.

【考点】勾股定理的应用;全等三角形的判定与性质.
【分析】根据全等三角形的判定方法得出△CAD≌△EAB(SAS),进而利用全等三角形的性质结合勾股定理得出DC的长,进而得出答案.
【解答】解:探索:BE=CD,
理由:∵∠BAD=∠CAE=90°,
∴∠CAD=∠EAB,
在△CAD和△EAB中
∵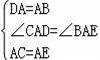
 ,
,
∴△CAD≌△EAB(SAS);
应用:如图②,过点A作AD⊥AB,且AD=AB,连接BD,
由探索,得△CAD≌△EAB,
∴BE=DC,
∵AD=AB=100m,∠DAB=90°,
∴∠ABD=45°,BD=100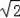
 m,
m,
∵∠ABC=45°,
∴∠DBC=90°,
在Rt△DBC中,BC=100m,BD=100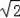
 m,
m,
∴CD=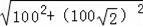
 =100
=100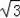
 (m),
(m),
则BE=100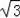
 m,
m,
答:BE的长为100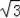
 m.
m.

【点评】此题主要考查了全等三角形的判定与性质以及勾股定理应用,正确得出△CAD≌△EAB(SAS)是解题关键.

在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
 B.
B.
 D.
D.





 路为普通公路,其余路段为高速公路,已知汽车在普通公路上行驶的速度为60km/h,在高速路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h,普通公路和高速公路各是多少km?
路为普通公路,其余路段为高速公路,已知汽车在普通公路上行驶的速度为60km/h,在高速路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h,普通公路和高速公路各是多少km? ,
, 为
为 的导函数,则
的导函数,则
 ,
, ,
, ,则( )
,则( ) B.
B. C.
C. D.
D.