题目内容
如图1,在直角梯形ABCD中,AD∥BC,∠B=∠A=90°,AD=a,BC=b,AB=c,
操作示例:
我们可以取直角梯形ABCD的非直角腰CD的中点P,过点P作PE∥AB,裁掉△PEC,并将△PEC绕点P逆时针旋转180°拼接到△PFD的位置,构成新的图形(如图2).
思考发现:
判断图2中四边形ABEF的形状: ;四边形ABEF的面积是 。(用含字母的代数式表示)
实践探究:
类比图2的剪拼方法,请你就图3(已知:AB∥DC)画出剪拼成一个平行四边形的示意图.
联想拓展:
小明通过探究后发现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
如图4,在梯形ABCD中,AD∥BC,E是CD的中点, EF⊥AB于点F,AB=5,EF=4,求梯形ABCD的面积。
如图5的多边形中,AE=CD,AE∥CD,能否象上面剪切方法一样沿一条直线进行剪切,拼成一平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.
略
解析:思考发现:四边形ABEF为矩形-------1分;四边形ABEF的面积是---2分
实践探究:
联想拓展:
(1)如图4过点E作PE∥AB交BC与P交AD的延长线于Q,
则有S梯形ABCD=S□ ABPQ= AB ×EF =5×4=20 -------5分
(2)
作图-------7分
取AB的中点F,BC的中点G,作直线FG分别交AE,CD于点P,Q,
则可拼成一平行四边形PQDE ------8分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
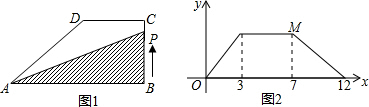
 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )| A、3 | B、4 | C、5 | D、6 |