题目内容
 如图,已知DE∥AB,那么表示∠3的式子是
如图,已知DE∥AB,那么表示∠3的式子是
- A.∠1+∠2-180°
- B.∠1-∠2
- C.180°+∠1-∠2
- D.180°-2∠1+∠2
A
分析:过点C作CG∥AB,因为AB∥EF,所以CG∥EF,利用两直线平行,同旁内角互补,内错角相等求出∠1+∠BCG=180°,∠3=∠DCG,再利用角之间的和差关系求解.
解答: 解:过点C作CG∥AB,
解:过点C作CG∥AB,
∵AB∥EF,
∴CG∥EF,
∴∠1+∠BCG=180°,∠3=∠DCG,
又∵∠2=∠BCG+∠GCD,
∴∠3=∠DCG=∠1+∠2-(∠1+∠BCG)=∠1+∠2-180°.
故选A.
点评:本题主要考查作辅助线构造三条互相平行的直线,然后利用平行线的性质和角的和差关系求解.
分析:过点C作CG∥AB,因为AB∥EF,所以CG∥EF,利用两直线平行,同旁内角互补,内错角相等求出∠1+∠BCG=180°,∠3=∠DCG,再利用角之间的和差关系求解.
解答:
 解:过点C作CG∥AB,
解:过点C作CG∥AB,∵AB∥EF,
∴CG∥EF,
∴∠1+∠BCG=180°,∠3=∠DCG,
又∵∠2=∠BCG+∠GCD,
∴∠3=∠DCG=∠1+∠2-(∠1+∠BCG)=∠1+∠2-180°.
故选A.
点评:本题主要考查作辅助线构造三条互相平行的直线,然后利用平行线的性质和角的和差关系求解.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
 10、如图,已知DE∥AB,则AC:DC=
10、如图,已知DE∥AB,则AC:DC=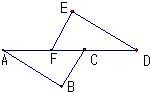 19、如图:已知DE=AB,∠D=∠A,请你补充一个条件,使△ABC≌△DEF,并说明你判断的理由:
19、如图:已知DE=AB,∠D=∠A,请你补充一个条件,使△ABC≌△DEF,并说明你判断的理由: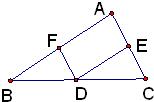 32、如图,已知DE∥AB,DF∥AC,∠EDF=85°,∠BDF=63°.
32、如图,已知DE∥AB,DF∥AC,∠EDF=85°,∠BDF=63°. 5、如图,已知DE∥AB,那么表示∠3的式子是( )
5、如图,已知DE∥AB,那么表示∠3的式子是( ) 19、如图:已知DE=AB,∠D=∠A,请你补充一个条件,使△ABC≌△DEF,并说明你判断的理由:
19、如图:已知DE=AB,∠D=∠A,请你补充一个条件,使△ABC≌△DEF,并说明你判断的理由: