题目内容
如图，直线
与
轴、
轴分别交于A、B两点，把△OAB绕点O顺时针旋转90°得到△OCD．⑴在图中画出△OCD；
⑵求经过A、B、D三点的抛物线的解析式；
⑶点P在抛物线对称轴上运动
①当直线CP把△OCD分成面积相等的两部分时，试求出点P的坐标；
②是否存在点P，使
为直角三角形，若存在，请求出点
的坐标；如果不存在，请说明理由．
解：(1)画图见图………1分
⑵由已知可知：
A（-2，0）、B（0，4）、C（0，2）、D（4，0）
设经过A、B、D的抛物线解析式为
则有：
①
②
③
解①②③得：
，
，………2分
∴抛物线的解析式为：
………3分
⑶①若存在点P满足条件，则直线CP必经过OD的中点E（2，0）
易知经过C、E的直线为
于是点P的坐标为P（1，1）………5分
②点C（0，2）、D（4，0）、P（1, m）
若
则
，即
，
解得
,
…….7分
若
则
，即
，解得
…….8分
若
则
，即
，解得
…….9分
综上所述，存在点使为直角三角形，
，，
，
…….10分解析:
略
⑵由已知可知：
A（-2，0）、B（0，4）、C（0，2）、D（4，0）
设经过A、B、D的抛物线解析式为
则有：
① ② ③ 解①②③得：
，，………2分∴抛物线的解析式为：
………3分⑶①若存在点P满足条件，则直线CP必经过OD的中点E（2，0）
易知经过C、E的直线为
于是点P的坐标为P（1，1）………5分
②点C（0，2）、D（4，0）、P（1, m）
若
则
，即，解得
,…….7分若
则
，即，解得…….8分若
则
，即，解得…….9分综上所述，存在点
使为直角三角形，，，，…….10分解析:略
练习册系列答案
相关题目
与
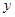轴的交点坐标为A（0,1），与
轴的交点坐标为B（-3,0）；P、Q分别是
S四边形OQPB时，请确定点P在AB上的位置，并求出线段PQ的长；
与
轴、
轴分别交于A、B两点，动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动． 动直线EF从
与
轴、
轴分别交于A、B两点，动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动．
动直线EF从
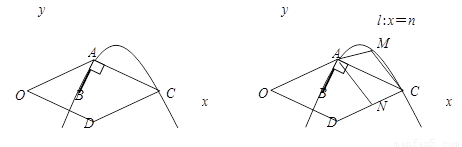（3）如图2，设垂直于x轴的直线l：x＝n与（2）中所求的抛物线交于点M，与CD交于点N，若直线l 沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间时，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．