Question

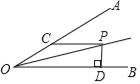
【题目】如图，已知∠AOB＝30°，P是∠AOB平分线上一点，CP∥OB，交OA于点C，PD⊥OB，垂足为点D，且PC＝8，则PD的长为_____．

Answer 1

【答案】4

【解析】

过点P作PE⊥OA于点E，根据角平分线上的点到角的两边的距离相等可得PE=PD，再根据两直线平行，内错角相等可得∠POD=∠OPC，根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=∠AOB，再根据直角三角形30°角所对的直角边等于斜边的一半得出PE=PC=4，根据角平分线的性质得到答案．

解：作PE⊥OA于E，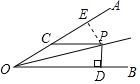

∵P是∠AOB平分线上一点，
∴∠AOP=∠BOP=15°，
∵PC∥OB，
∴∠POD=∠OPC，
∴∠PCE=∠POC+∠OPC=∠POC+∠POD=∠AOB=30°，
∴PE=PC=4，
∵P是∠AOB平分线上一点，PD⊥OB，PE⊥OA，
∴PD=PE=4，
故答案为：4．