Question

如图，在直角坐标系中，点D在x轴上，⊙D与y轴相切于原点O，与x轴交于点E，与直线y=-

3

3

x+1相切于F点，该直线与y轴、x轴分别相交于A、B两点，求由

EF

和线段FB、EB所围成的阴影部分的面积．

Answer 1

考点：一次函数的性质,勾股定理,切线的性质,扇形面积的计算

专题：计算题

分析：连结DF，如图，设⊙O的半径为r，先利用直线解析式确定A（0，1、B（

3

，0），再利用勾股定理计算出AB=2，则∠ABO=30°，接着根据切线的性质得到OD=r，DF⊥AB，
然后在Rt△BDF中根据含30度的直角三角形三边的关系得到BD=2DF=2r，BF=

3

DF=

3

r，且∠BDF=60°，由于OD+BD=OB，即r+2r=

3

，解得r=

3

3

，所以DF=

3

3

，BF=1，
然后根据扇形面积公式和阴影部分的面积=S_△BDF-S_扇形EDF进行计算．

解答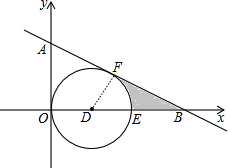：解：连结DF，如图，设⊙O的半径为r，
当x=0时，y=-

3

3

x+1=1，则A（0，1）；当y=0时，-

3

3

x+1=0，解得x=

3

，则B点坐标为（

3

，0），
在Rt△AOB中，AB=

OA2+OB2

=2，
∴∠ABO=30°，
∵⊙D与y轴相切于原点O，与直线y=-

3

3

x+1相切于F点，
∴OD=r，DF⊥AB，
在Rt△BDF中，∵∠DBF=30°
∴BD=2DF=2r，BF=

3

DF=

3

r，∠BDF=60°，
而OD+BD=OB，
∴r+2r=

3

，解得r=

3

3

，
∴DF=

3

3

，BF=1，
∴阴影部分的面积=S_△BDF-S_扇形EDF
=

1

2

•

3

3

•1-

60•π•( 3 3 )2

360

=

3 3 -π

18

．

点评：本题考查了一次函数的性质：k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降．由于y=kx+b与y轴交于（0，b），当b＞0时，（0，b）在y轴的正半轴上，直线与y轴交于正半轴；当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．也考查了切线的性质和扇形的面积公式．