Question

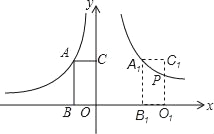
【题目】一副直角三角板由一块含30°的直角三角板与一块等腰直角三角板组成，且含30°角的三角板的较长直角边与另一三角板的斜边相等（如图1）

（1）如图1，这副三角板中，已知AB＝2，AC＝　 　，A′D＝　 　

（2）这副三角板如图1放置，将△A′DC′固定不动，将△ABC通过旋转或者平移变换可使△ABC的斜边BC经过△A′DC′′的直角顶点D．

方法一：如图2，将△ABC绕点C按顺时针方向旋转角度α（0°＜α＜180°）

方法二：如图3，将△ABC沿射线A′C′方向平移m个单位长度

方法三：如图4，将△ABC绕点A按逆时针方向旋转角度β（0°＜β＜180°）

请你解决下列问题：

①根据方法一，直接写出α的值为：　 　；

②根据方法二，计算m的值；

③根据方法三，求β的值．

（3）若将△ABC从图1位置开始沿射线A′C′平移，设AA′＝x，两三角形重叠部分的面积为y，请直接写出y与x之间的函数关系式和相应的自变量x的取值范围．

Answer 1

【答案】（1）；（2）①15°；②；③30°；（3）

【解析】

（1）根据直角三角形中30°的直角边所对的直角边等于斜边的一半，即可求得BC的长，然后根据勾股定理即可求得AC的长；

（2）①根据三角板的度数即可求解；

②作DH⊥A′C于H，易证△CDH∽△CBA，根据相似三角形的对应边的比相等，即可求得CH的长，进而求得CC′；

③作DH⊥A′C′于H，AG⊥BC于G，可以证得Rt△AGD≌Rt△DHA，则BC∥AC′，利用平行线的性质即可求解；

（3）分0＜x≤，＜x≤，＜x≤2，x＞2四种情况即可求解．

（1）∵直角△ABC中，∠BAC＝30°，

∴BC＝2AB＝4，

∴AC＝＝2，

在等腰直角直角△A′DC′中，A′C′＝2，

∴A′D＝A′C′＝；

（2）①α＝45°﹣30°＝15°；

②作DH⊥A′C于H，则DH＝A′C′＝C′H＝，

∵DH∥AB，

∴△CDH∽△CBA．

∴，即，

∴CH＝3．

∴CC′＝CH﹣C′H＝3﹣，即m＝CC′＝3﹣；

③作DH⊥A′C′于H，AG⊥BC于G，

由已知：DH＝，

AG×BC＝AB×AC，

∴AG＝＝，

∴AG＝DH．

在Rt△AGD和Rt△DHA中：，

∴Rt△AGD≌Rt△DHA，

∴∠GDA＝∠DAH＝45°，

∴BC∥AC′，

∴β＝∠BCA＝30°；

（3）y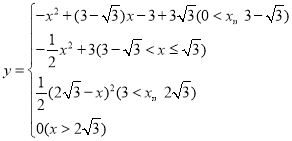＝．