题目内容
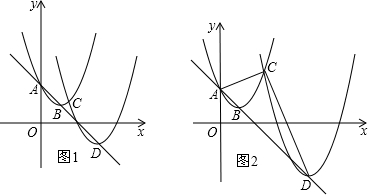
（2013•台州）如图，在⊙O中，过直径AB延长线上的点C作⊙O的一条切线，切点为D．若AC=7，AB=4，则sinC的值为| 2 |
| 5 |
| 2 |
| 5 |
分析：连接OD，根据切线的性质可得∠ODC=90°，可得sin∠C=
即可求解．
| OD |
| OC |
解答：
解：连接OD，
∵CD是⊙O的切线，
∴∠ODC=90°，
∵AC=7，AB=4，
∴半径OA=2，
则OC=AC-AO=7-2=5，
∴sinC=
=
．
故答案为：
．
解：连接OD，∵CD是⊙O的切线，
∴∠ODC=90°，
∵AC=7，AB=4，
∴半径OA=2，
则OC=AC-AO=7-2=5，
∴sinC=
| OD |
| OC |
| 2 |
| 5 |
故答案为：
| 2 |
| 5 |
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
（2013•台州）如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2、中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（ ）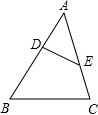
（2013•台州）如图，在△ABC中，点D，E分别在边AB，AC上，且
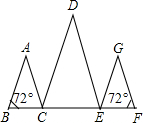（2013•台州）如图，点B，C，E，F在一直线上，AB∥DC，DE∥GF，∠B=∠F=72°，则∠D=
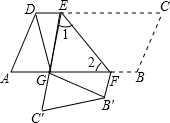（2013•台州）如图，在?ABCD中，点E，F分别在边DC，AB上，DE=BF，把平行四边形沿直线EF折叠，使得点B，C分别落在B′，C′处，线段EC′与线段AF交于点G，连接DG，B′G．