题目内容
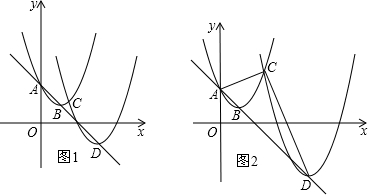
（2013•台州）如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2、中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（ ）分析：首先得到当点E旋转至y轴上时DE最小，然后分别求得AD、OE′的长，最后求得DE′的长即可．
解答：
解：如图，当点E旋转至y轴上时DE最小；
∵△ABC是等边三角形，D为BC的中点，
∴AD⊥BC
∵AB=BC=2
∴AD=AB•cos∠B=
，
∵正六边形的边长等于其半径，正六边形的边长为2，
∴OE=OE′=2
∵点A的坐标为（0，6）
∴OA=6
∴D′E=OA-AD-OE′=4-
故选B．
解：如图，当点E旋转至y轴上时DE最小；∵△ABC是等边三角形，D为BC的中点，
∴AD⊥BC
∵AB=BC=2
∴AD=AB•cos∠B=
| 3 |
∵正六边形的边长等于其半径，正六边形的边长为2，
∴OE=OE′=2
∵点A的坐标为（0，6）
∴OA=6
∴D′E=OA-AD-OE′=4-
| 3 |
故选B．
点评：本题考查了正多边形的计算及等边三角形的性质，解题的关键是从图形中整理出直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
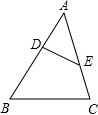（2013•台州）如图，在△ABC中，点D，E分别在边AB，AC上，且
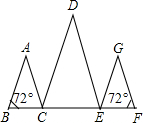（2013•台州）如图，点B，C，E，F在一直线上，AB∥DC，DE∥GF，∠B=∠F=72°，则∠D=
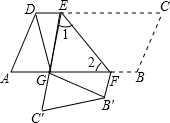（2013•台州）如图，在?ABCD中，点E，F分别在边DC，AB上，DE=BF，把平行四边形沿直线EF折叠，使得点B，C分别落在B′，C′处，线段EC′与线段AF交于点G，连接DG，B′G．