Question

【题目】A、B两个港口相距100海里，港口B在港口A的北偏东31°方向上，有一艘船从A港口出发，沿北偏西44°方向匀速行驶3小时后，到达位于B港口南偏西76°方向的C处．求此船行驶的速度（结果精确到1海里/时，参考数据：≈1.414，≈1.732，≈2.449）

Answer 1

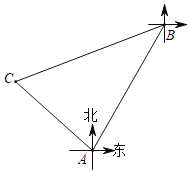
【答案】27海里/时

【解析】

利用方向角的定义得到∠1＝∠2＝31°，则∠BAC＝31°+44°＝75°，∠ABC＝76°﹣31°＝45°，在利用三角形内角和得到∠ACB＝60°，作AH⊥BC于H，如图，在Rt△ABH中，利用等腰直角三角形的性质得BH＝AH＝50在Rt△ACH中，利用含30度的直角三角形三边的关系得到CH＝AH＝，AC＝2CH＝，然后计算此船行驶的速度．

根据题意得∠1＝∠2＝31°，

∠BAC＝31°+44°＝75°，∠ABC＝76°﹣31°＝45°，

∴∠ACB＝180°﹣75°﹣45°＝60°，

作AH⊥BC于H，如图，

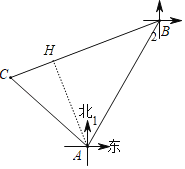
在Rt△ABH中，BH＝AH＝AB＝50，

在Rt△ACH中，CH＝AH＝×50＝，

AC＝2CH＝，

∴此船行驶的速度＝＝≈27．

答：此船行驶的速度为27海里/时．