题目内容
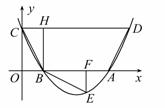
如图,抛物线与![]() 轴交于
轴交于![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)两点,且
,0)两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 是方程
是方程![]() 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)点![]() 在(1)中抛物线上,点
在(1)中抛物线上,点![]() 为抛物线上一动点,在
为抛物线上一动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点![]() 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
 |
(1)∵![]() ,∴
,∴![]() ,
,![]() 。
。
∴![]() ,
,![]() 。····················1分
。····················1分
又∵抛物线过点![]() 、
、![]() 、
、![]() ,
,
故设抛物线的解析式为![]() ,
,
将点![]() 的坐标代入,求得
的坐标代入,求得![]() 。
。
∴抛物线的解析式为![]() 。········3分
。········3分
(2)设点![]() 的坐标为(
的坐标为(![]() ,0),过点
,0),过点![]() 作
作![]() 轴于点
轴于点![]() (如图(1))。
(如图(1))。
∵点![]() 的坐标为(
的坐标为(![]() ,0),点
,0),点![]() 的坐标为(6,0),
的坐标为(6,0),
∴![]() ,
,![]() 。···························4分
。···························4分
∵![]() ,∴
,∴![]() 。
。
∴![]() ,∴
,∴![]() ,∴
,∴![]() 。·················5分
。·················5分
 ∴
∴![]()
![]() ······6分
······6分
![]() 。
。
∴当![]() 时,
时,![]() 有最大值4。
有最大值4。
此时,点![]() 的坐标为(2,0)。··············7分
的坐标为(2,0)。··············7分
(3)∵点![]() (4,
(4,![]() )在抛物线
)在抛物线![]() 上,
上,
 ∴当
∴当![]() 时,
时,![]() ,
,
∴点![]() 的坐标是(4,
的坐标是(4,![]() )。
)。
如图(2),当![]() 为平行四边形的边时,
为平行四边形的边时,![]()
![]()
![]()
![]() ,
,
∵![]() (4,
(4,![]() ),∴
),∴![]() (0,
(0,![]() ),
),![]() 。
。
∴![]() ,
,![]() 。 ··········9分
。 ··········9分
① 如图(3),当![]() 为平行四边形的对角线时,
为平行四边形的对角线时,
设![]() ,则平行四边形的对称中心为
,则平行四边形的对称中心为
(![]() ,0)。·················10分
,0)。·················10分
∴![]() 的坐标为(
的坐标为(![]() ,4)。
,4)。
把![]() (
(![]() ,4)代入
,4)代入![]() ,得
,得![]() 。
。
解得 ![]() 。
。
![]() ,
,![]() 。
。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
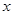 轴交于
轴交于 (2)点
(2)点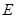 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以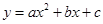 与
与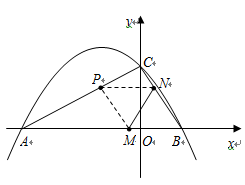
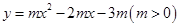 与
与 轴交于
轴交于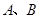 两点,与
两点,与 轴交于
轴交于 点.
点.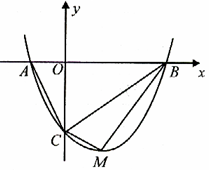
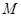 的坐标(用含
的坐标(用含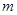 的代数式表示),
的代数式表示), 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;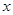 轴交于
轴交于 (
( ,0)、
,0)、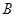 (
( ,0)两点,且
,0)两点,且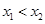 ,与
,与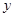 轴交于点
轴交于点 ,其中
,其中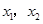 是方程
是方程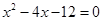 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段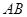 上的一个动点,过点
上的一个动点,过点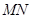 ∥
∥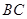 ,交
,交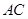 于点
于点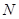 ,连接
,连接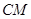 ,当
,当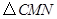 的面积最大时,求点
的面积最大时,求点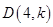 在(1)中抛物线上,
在(1)中抛物线上, 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以 为顶
为顶