Question

【题目】如图，已知∠AOB=60°，半径为2的⊙M与边OA、OB相切，若将⊙M水平向左平移，当⊙M与边OA相交时，设交点为E和F，且EF=6，则平移的距离为（　　）

A. 2 B. 2或6 C. 4或6 D. 1或5

Answer 1

【答案】B

【解析】

本题分圆心M在OA的左边和右边两种情况求解即可.

当将⊙M水平向左平移，当点M运动到M′位置时，如图1：

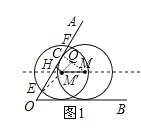
作MC⊥OA于C点，M′H⊥OA于H，M′Q⊥MC于Q，连结M′E，

∵⊙M与边OB、OA相切，

∴MM′∥OB，MC=2，

∵M′H⊥OA，

∴EH=FH=EF=×6=3，

在Rt△EHM′中，EM′=2，

∴HM′== ，

∵M′Q⊥MC，

∴四边形M′QCH为矩形，

∴CQ=M′H=，

∴MQ=2-=，

∵∠QM′M=∠AOB=60°，

∴∠QM′M=30°，

∴M′Q=MQ=1，

∴MM′=2；

当将⊙M水平向左平移，当点M运动到M″位置时，如图2，

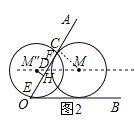
作MC⊥OA于C点，M″H⊥OA于H，M″M交OA于D点，

易得MC=2，M″H=，

∵∠MDC=∠M″DH=∠AOB=60°，

∴∠HM″D=30°，∠CMD=30°，

在Rt△CDM中，CM=2，则DC=2， DM=4，

在Rt△HM″D中，M″H =，则DH=1，M″D=2，

∴MM″= DM+ M″D =4+2=6，

综上所述，当⊙M平移的距离为2或6．故选：B.