题目内容
 如图,将Rt△ABC绕直角顶点C旋转至Rt△A′B′C,并使B′,B,A′同在一直线上,若∠A=α,则旋转角度∠ACA′是
如图,将Rt△ABC绕直角顶点C旋转至Rt△A′B′C,并使B′,B,A′同在一直线上,若∠A=α,则旋转角度∠ACA′是
- A.α
- B.
 α
α - C.2α
- D.3α
C
分析:由Rt△ABC中,∠A=α,即可求得∠B的度数,又由将Rt△ABC绕直角顶点C旋转至Rt△A′B′C,并使B′,B,A′同在一直线上,根据旋转的性质,可得∠B′=∠ABC=90°-α,BC=B′C,继而求得旋转角∠BCB′的度数,则可求得答案.
解答:∵Rt△ABC中,∠A=α,
∴∠ABC=90°-α,
∵将Rt△ABC绕直角顶点C旋转至Rt△A′B′C,并使B′,B,A′同在一直线上,
∴∠B′=∠ABC=90°-α,BC=B′C,
∴∠CBB′=∠B′=90°-α,
∴∠BCB′=180°-∠B′-∠CBB′=2α,
∴∠ACA′=∠BCB′=2α.
故选C.
点评:此题考查了旋转的性质、等腰三角形的性质以及三角形内角和定理.此题难度不大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.
分析:由Rt△ABC中,∠A=α,即可求得∠B的度数,又由将Rt△ABC绕直角顶点C旋转至Rt△A′B′C,并使B′,B,A′同在一直线上,根据旋转的性质,可得∠B′=∠ABC=90°-α,BC=B′C,继而求得旋转角∠BCB′的度数,则可求得答案.
解答:∵Rt△ABC中,∠A=α,
∴∠ABC=90°-α,
∵将Rt△ABC绕直角顶点C旋转至Rt△A′B′C,并使B′,B,A′同在一直线上,
∴∠B′=∠ABC=90°-α,BC=B′C,
∴∠CBB′=∠B′=90°-α,
∴∠BCB′=180°-∠B′-∠CBB′=2α,
∴∠ACA′=∠BCB′=2α.
故选C.
点评:此题考查了旋转的性质、等腰三角形的性质以及三角形内角和定理.此题难度不大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
相关题目
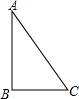 如图,将Rt△ABC绕直角边AB旋转一周,所得的几何体的主视图是( )
如图,将Rt△ABC绕直角边AB旋转一周,所得的几何体的主视图是( )A、 | B、 | C、 | D、 |
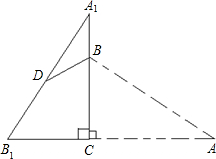 如图,将Rt△ABC绕直角顶点C逆时针旋转90°到△A1B1C的位置,已知AC=4cm,BC=3cm,设D是A1B1的中点,连接BD,则BD的长为
如图,将Rt△ABC绕直角顶点C逆时针旋转90°到△A1B1C的位置,已知AC=4cm,BC=3cm,设D是A1B1的中点,连接BD,则BD的长为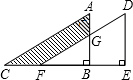 如图,将Rt△ABC沿CB的方向平移BE距离后得到Rt△DEF,已知AG=2,BE=4,DE=8,则阴影部分的面积是
如图,将Rt△ABC沿CB的方向平移BE距离后得到Rt△DEF,已知AG=2,BE=4,DE=8,则阴影部分的面积是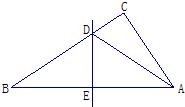 26、如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
26、如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.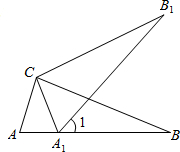 如图,将Rt△ABC绕直角顶点C旋转到Rt△A1B1C,若点A1落在AB边上,且∠B=20°,∠1=
如图,将Rt△ABC绕直角顶点C旋转到Rt△A1B1C,若点A1落在AB边上,且∠B=20°,∠1=