Question

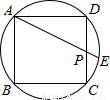
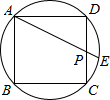如图，已知边长为1圆内接正方形ABCD中，P为CD的中点，连接AP并延长交圆于点E，则DE的长为

10

5

．

Answer 1

分析：连接CE，作出EF⊥CD，运用相似三角形的性质，得出EF，PF的长，再根据勾股定理即可得出结论．

解答：解：连接CE，作EF⊥PF
∵∠DAP=∠PCE，∠APD=∠CPE，
∴△APD∽△CPE，
∴

AP

CP

=

DP

PE

∴

5 2

1 2

=

1 2

PE

，
∴PE=

5

10

，
∵FE∥AD
∴△APD∽△EPF，
∴

AP

PE

=

DP

PF

，
∴

5 2

5 10

=

1 2

PF

，
∴PF=

1

10

，
∴EF=

PE2-PF2

=

( 5 10 )2-( 1 10 )2

=

1

5

，
∴DE=

EF2+(PD+PF)2

=

( 1 5 )2+( 1 2 + 1 10 )2

=

10

5

．

点评：本题考查的是正多边形的圆及相似三角形的判定与性质，根据题意作出辅助线，构造出相似三角形是解答此题的关键．