题目内容
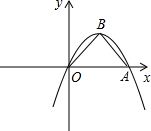 如图,二次函数y=ax2+bx的图象经过点A(4,0)、B(2,2),连接OB、AB.
如图,二次函数y=ax2+bx的图象经过点A(4,0)、B(2,2),连接OB、AB.(1)求a,b;
(2)将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,则线段A′B′的中点P的坐标为
分析:(1)利用二次函数y=ax2+bx的图象经过点A(4,0)、B(2,2),直接将两点代入解析式求出即可;
(2)首先求出OB,AB的长度,再画出旋转后的图象,进而求出B′P,OB′的长,从而表示出其坐标,再代入解析式即可判断出是否在图象上.
(2)首先求出OB,AB的长度,再画出旋转后的图象,进而求出B′P,OB′的长,从而表示出其坐标,再代入解析式即可判断出是否在图象上.
解答: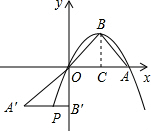 解:(1)由题意得
解:(1)由题意得
,
解得
;
(2)作BC⊥OA,垂足为C,
∵A,B点的坐标为A(4,0),(2,2)
∴OB=AB,
∴CO=BC=CA=2,
∵将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,
∴OB=OB′=2
,B′P=
AB=
,
∴线段A′B′的中点P的坐标为:P(-
,-2
),
当x=-
时,y=-
×(-
)2+2×(-
)=-1-2
≠-2
.
所以点P不在此二次函数的图象上.
 解:(1)由题意得
解:(1)由题意得
|
解得
|
(2)作BC⊥OA,垂足为C,
∵A,B点的坐标为A(4,0),(2,2)
∴OB=AB,
∴CO=BC=CA=2,
∵将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,
∴OB=OB′=2
| 2 |
| 1 |
| 2 |
| 2 |
∴线段A′B′的中点P的坐标为:P(-
| 2 |
| 2 |
当x=-
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
所以点P不在此二次函数的图象上.
点评:此题主要考查了二次函数的综合应用以及旋转图形的性质,根据旋转图形的性质画出图象再求出对应线段长度是解决问题的关键.

练习册系列答案
相关题目
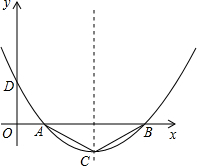 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b