题目内容
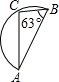如图，AB是半圆的直径，∠ABC=63°，则 | BC |
分析：由于AB是半圆的直径，根据圆周角定理的推论，易知∠ACB=90°，则∠A与∠ABC互余，由此可求得∠A的度数，即
所对的圆周角的度数．
|
| BC |
解答：解：∵AB是半圆的直径，
∴∠ACB=90°；
∴∠A+∠ABC=90°，
即∠A=90°-∠ABC=27°；
故
所对的圆周角的度数是27°．
故答案为：27．
∴∠ACB=90°；
∴∠A+∠ABC=90°，
即∠A=90°-∠ABC=27°；
故
|
| BC |
故答案为：27．
点评：此题主要考查的是圆周角定理的推论：半圆（或直径）所对的圆周角是直角．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
道BC的长86.96米，跑道的宽为l米．（π=3.14，结果精确到0.01）
