题目内容
如图,反比例函数 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
(3)求△AOB的面积.
(1)y=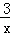 y=x+2
y=x+2
(2)x<﹣3或0<x<1
(3)4
解析试题分析:(1)把A(1,3)代入反比例函数 即可得到k=3,然后把B(n,﹣1)代入y=
即可得到k=3,然后把B(n,﹣1)代入y=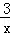 求出n,再把A点和B点坐标代入y=mx+b中得到关于m、b的方程组,然后解方程组即可;
求出n,再把A点和B点坐标代入y=mx+b中得到关于m、b的方程组,然后解方程组即可;
(2)观察图象可得到当x<﹣3或0<x<1时,反比例函数的图象都在一次函数的图象的上方;
(3)先求出直线AB与x轴的交点C的坐标,则S△OAB=S△OAC+S△OBC,然后利用三角形的面积公式计算即可.
解:(1)把A(1,3)代入反比例函数 ,
,
∴k=1×3=3,
∴反比例函数的解析式为y=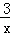 ,
,
把B(n,﹣1)代入y=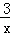 得,n=﹣3,
得,n=﹣3,
∴点B的坐标为(﹣3,﹣1),
把A(1,3)、点B(﹣3,﹣1)代入一次函数y=mx+b得,m+b=3,﹣3m+b=﹣1,解得m=1,b=2,
∴一次函数的解析式为y=x+2;
(2)当x<﹣3或0<x<1时,反比例函数的值大于一次函数的值;
(3)连OA、OB,直线AB交x轴与C点,如图,
对于y=x+2,令y=0,x=﹣2,
∴C点坐标为(﹣2,0),
∴S△OAB=S△OAC+S△OBC= ×2×3+
×2×3+ ×2×1=4.
×2×1=4.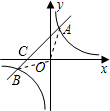
点评:本题考查了反比例函数与一次函数的交点问题:同时满足反比例函数的解析式和一次函数的解析式的点的坐标为它们图象的交点坐标.也考查了待定系数法求函数的解析式以及坐标轴上点的坐标特点.

某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
| 年度 | 2009 | 2010 | 2011 | 2012 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
(1)(4分)左下图是有几个大小完全一样的小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,请你画出该几何体的主视图和左视图.

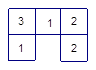
|
|
(2)(6分)如图,点P是
 的边OB上的一点
的边OB上的一点①过点P画OB的垂线,交OA于点C
②过点P画OA的垂线,垂足为H
③线段PH的长度是点P到 的距离,
是点C到直线OB的距离。
因为 所以线段PC、PH、OC这三条线段大小关系是 (用“<”号连接)
(23--25题每题8分,共24分)

 个单位后,使点B恰好落在双曲线上,求
个单位后,使点B恰好落在双曲线上,求 的图象有一个交点A(m,2).
的图象有一个交点A(m,2).
 交于点C(1,6)、D(3,n)两点,
交于点C(1,6)、D(3,n)两点, 轴于点E,
轴于点E, 轴于点F.
轴于点F.
 ,
, ;
; .
.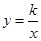 的图象交于A、B两点。
的图象交于A、B两点。