题目内容
如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE AC,与BD的垂线DE交于点E,
AC,与BD的垂线DE交于点E,
(1)求证:△ABC≌△BDE
(2)三角形BDE可由三角形ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法)

【答案】
(1)见解析
(2)见解析
【解析】三角形内角和定理,全等三角形的判定,作图(旋转变换),线段垂直平分线的性质。
(1)利用已知得出∠A=∠DBE,从而利用ASA得出△ABC≌△BDE即可。
证明:在Rt△ABC中,∵∠ABC=90°,∴∠ABE+∠DBE=90°。
∵BE⊥AC,∴∠ABE+∠A=90°。∴∠A=∠DBE。
∵DE是BD的垂线,∴∠D=90°。
在△ABC和△BDE中,∵ ∠A=∠DBE ,AB=DB ,∠ABC=∠D,
∴△ABC≌△BDE(ASA)。
(2)利用垂直平分线的性质可以作出,或者利用正方形性质得出旋转中心也可。
如图,点O就是所求的旋转中心。


练习册系列答案
相关题目
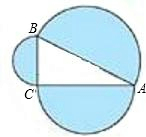 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
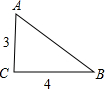
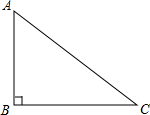 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.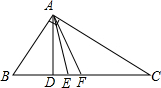 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=