题目内容
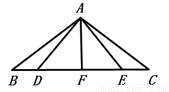
如图,AE,AD分别是△ABC的高和角平分线,且∠B=40°,∠C=60°,求∠BAD和∠DAE的度数.

【解析】
∵∠B=40°,∠C=60°
∴∠BAC=180°-∠B-∠C=80°
∵AD是△ABC的高
∴∠AEC=90°
∴∠EAC=180°-90°-∠C=30°
∵AE是△ABC的角平分线
∴∠BAD=∠DAC= ∠BAC=40°
∠BAC=40°
∴∠DAE=∠DAC-∠EAC=40°-30°=10°
【解析】
试题分析:根据三角形的内角和定理得到∠BAC的度数,再利用角平分线的性质可求出∠BAD=∠DAC = ∠BAC,而∠EAC=90°-∠C,利用∠DAE=∠DAC-∠EAC进行计算即可.
∠BAC,而∠EAC=90°-∠C,利用∠DAE=∠DAC-∠EAC进行计算即可.
考点:三角形内角和定理;角平分线的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的一元二次方程
的一元二次方程 有两个不相等的实数根,则
有两个不相等的实数根,则 的取值范围是( ).
的取值范围是( ).  (B)
(B)
 且
且 ≠1 (D)
≠1 (D) 且
且

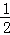 QC,若将这个正方体纸盒沿折线AP﹣PQ﹣QH裁剪并展开,得到的平面图形是( )
QC,若将这个正方体纸盒沿折线AP﹣PQ﹣QH裁剪并展开,得到的平面图形是( )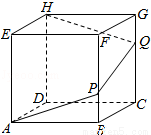
 CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )