题目内容
如图，在正方形ABCD中，M是BC边上的动点，N在CO上，且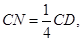
若AB=1，设BM=x,当x= 时，以A、B、M为顶点的三角形和以N、C、M为顶点的三角形相似．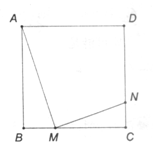
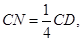若AB=1，设BM=x,当x= 时，以A、B、M为顶点的三角形和以N、C、M为顶点的三角形相似．
或
析：根据正方形的四条边都相等求出CN的长度，再根据相似三角形对应边成比例，分①CN与BM是对应边，②CN与AB是对应边两种情况列式求解即可．
解答：解：∵CN=1/4CD，AB=1，
∴CN=1/4×1=1/4，
∵BM=x，
∴CM=1-x，
①当CN与BM是对应边时，
=
，
即1/4X=(1-X)/1，
解得x=1/2，
②当CN与AB是对应边时，
CN/AB=CM/BM，
即1/4=(1-X)/X，
解得x=4/5．
综上所述，x的值是
或
故答案为：或．
解答：解：∵CN=1/4CD，AB=1，
∴CN=1/4×1=1/4，
∵BM=x，
∴CM=1-x，
①当CN与BM是对应边时，
=，即1/4X=(1-X)/1，
解得x=1/2，
②当CN与AB是对应边时，
CN/AB=CM/BM，
即1/4=(1-X)/X，
解得x=4/5．
综上所述，x的值是
或故答案为：
或．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
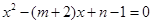的两根:
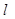交x轴于点D，试求直线
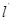分别交射线CA，CB（点C除外）于点M，N，则
的值是否为定值，若是，求出定值，若不是，请说明理由
0，4）、B（2，4），它的最高点纵坐标为
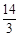，点P是第一象限抛物线上一点且PA=PO，过点P的直线分别交射线AB、x正半轴于C、D．设AC=m，OD=n．
米，已知引桥的坡度
，那么引桥的铅直高度为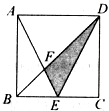
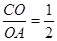，S△COD＝12，则△ABC的面积是 ．
