题目内容
已知多项式3x2+my-8与多项式-nx2+2y+7的差中，只含有常数项，求nm+m的值．
考点：整式的加减
专题：
分析：先列出两式相减的式子，再根据结果中只有常数项求出m、n的值，代入代数式进行计算即可．
解答：解：∵（3x2+my-8）-（-nx2+2y+7）
=3x2+my-8+nx2-2y-7
=（3+n）x2+（m-2）y-15，
∵结果中只有常数项，
∴3+n=0，m-2=0，
解得n=-3，m=2，
∴原式=（-3）2+2=11．
=3x2+my-8+nx2-2y-7
=（3+n）x2+（m-2）y-15，
∵结果中只有常数项，
∴3+n=0，m-2=0，
解得n=-3，m=2，
∴原式=（-3）2+2=11．
点评：本题考查的是整式的加减，熟知整式的加减实质上是合并同类项是解答此题的关键．
练习册系列答案
相关题目
已知平面直角坐标系中三点的坐标分别为：A（4、4），B（-2，2），C（3，0）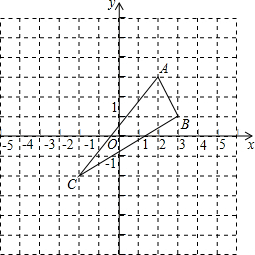
如图，已知△ABC的三个顶点分别为A（2，3）、B（3，1）、C（-2，-2）．