题目内容
如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:
 ,
, )
)
【答案】分析:(1))过点A作AC⊥OB于点C.可知△ABC为直角三角形.根据勾股定理解答.
(2)延长AB交l于D,比较OD与AM、AN的大小即可得出结论.
解答: 解(1)过点A作AC⊥OB于点C.由题意,得
解(1)过点A作AC⊥OB于点C.由题意,得
OA= 千米,OB=20千米,∠AOC=30°.
千米,OB=20千米,∠AOC=30°.
∴ (千米).(1分)
(千米).(1分)
∵在Rt△AOC中,OC=OA•cos∠AOC= =30(千米).
=30(千米).
∴BC=OC-OB=30-20=10(千米).…(3分)
∴在Rt△ABC中, =
= =20(千米).(5分)
=20(千米).(5分)
∴轮船航行的速度为: (千米/时).…(6分)
(千米/时).…(6分)
(2)如果该轮船不改变航向继续航行,不能行至码头MN靠岸. …(7分)
理由:延长AB交l于点D.
∵AB=OB=20(千米),∠AOC=30°.
∴∠OAB=∠AOC=30°,∴∠OBD=∠OAB+∠AOC=60°.
∴在Rt△BOD中,OD=OB•tan∠OBD=20×tan60°= (千米).…(9分)
(千米).…(9分)
∵ >30+1,
>30+1,
∴该轮船不改变航向继续航行,不能行至码头MN靠岸. …(10分)
点评:本题考查了解直角三角形的应用,此题结合方向角,考查了阅读理解能力、解直角三角形的能力.计算出相关特殊角和作出辅助线构造相似三角形是解题的关键.
(2)延长AB交l于D,比较OD与AM、AN的大小即可得出结论.
解答:
 解(1)过点A作AC⊥OB于点C.由题意,得
解(1)过点A作AC⊥OB于点C.由题意,得OA=
 千米,OB=20千米,∠AOC=30°.
千米,OB=20千米,∠AOC=30°.∴
 (千米).(1分)
(千米).(1分)∵在Rt△AOC中,OC=OA•cos∠AOC=
 =30(千米).
=30(千米).∴BC=OC-OB=30-20=10(千米).…(3分)
∴在Rt△ABC中,
 =
= =20(千米).(5分)
=20(千米).(5分)∴轮船航行的速度为:
 (千米/时).…(6分)
(千米/时).…(6分)(2)如果该轮船不改变航向继续航行,不能行至码头MN靠岸. …(7分)
理由:延长AB交l于点D.
∵AB=OB=20(千米),∠AOC=30°.
∴∠OAB=∠AOC=30°,∴∠OBD=∠OAB+∠AOC=60°.
∴在Rt△BOD中,OD=OB•tan∠OBD=20×tan60°=
 (千米).…(9分)
(千米).…(9分)∵
 >30+1,
>30+1,∴该轮船不改变航向继续航行,不能行至码头MN靠岸. …(10分)
点评:本题考查了解直角三角形的应用,此题结合方向角,考查了阅读理解能力、解直角三角形的能力.计算出相关特殊角和作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
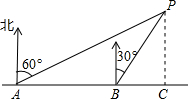 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.| A、250 | ||
| B、500 | ||
C、250
| ||
D、500
|
 如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)
如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号) 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC= 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC等于多少米?
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC等于多少米?