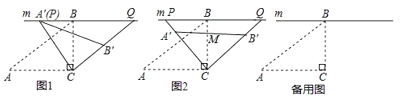
题目内容
【题目】如图,边长为5的正方形 ![]() 的顶点
的顶点![]() 在坐标原点处,点
在坐标原点处,点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是
是![]() 边上的点(不与点
边上的点(不与点![]() 重合)
重合)![]() ,且与正方形外角平分线
,且与正方形外角平分线![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)若点![]() 坐标为
坐标为![]() 时,①在
时,①在![]() 轴上是否存在点
轴上是否存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,求出点
是平行四边形?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②在平面内是否存在点![]() ,使四边形
,使四边形![]() 为正方形,若存在,请直接写出
为正方形,若存在,请直接写出![]() 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.
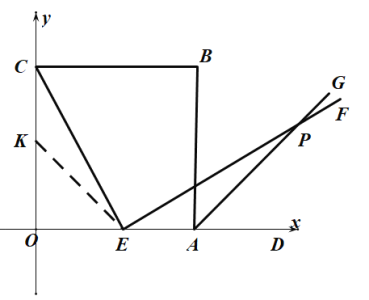
【答案】(1)见解析;(2)①存在,![]() ,理由见解析;②存在,
,理由见解析;②存在,![]() ,理由见解析
,理由见解析
【解析】
(1)在![]() 上截取
上截取![]() ,连结
,连结![]() ,利用正方形的性质,外角平分线和等量代换证明
,利用正方形的性质,外角平分线和等量代换证明![]() ,即可证明
,即可证明![]() ;
;
(2)过![]() 作
作![]() 交
交![]() 于
于![]() ,则点
,则点![]() 即为所求,利用平行四边形和正方形的性质证明
即为所求,利用平行四边形和正方形的性质证明![]() ,则有
,则有![]() ,进而可求出
,进而可求出![]() ,从而可确定M的坐标;
,从而可确定M的坐标;
(3)过点C作EP的平行线,过点P作CE的平行线,两平行线的交点即为所求Q点,过点Q作![]() 交CB与点K, 利用正方形的性质证明
交CB与点K, 利用正方形的性质证明![]() ,则有
,则有![]() 进而可求
进而可求![]() ,从而可确定Q的坐标.
,从而可确定Q的坐标.
(1)证明:在![]() 上截取
上截取![]() ,连结
,连结![]() ,
,
∵![]() 是正方形,
是正方形,
∴![]() ,
,
![]() ,
,
∴![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
∴![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
∵AG平分![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)①存在点![]() 使四边形
使四边形![]() 为平行四边形,
为平行四边形,
过![]() 作
作![]() 交
交![]() 于
于![]() ,则点
,则点![]() 即为所求,
即为所求,

∵![]() 是正方形,
是正方形,
∴![]() .
.
∵四边形![]() 为平行四边形,
为平行四边形,
![]() .
.
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 轴上存在点
轴上存在点![]() ,使四边形
,使四边形![]() 的平行四边形;
的平行四边形;
②存在点Q使四边形![]() 为正方形.
为正方形.
过点C作EP的平行线,过点P作CE的平行线,两平行线的交点即为所求Q点,过点Q作![]() 交CB与点K,
交CB与点K,
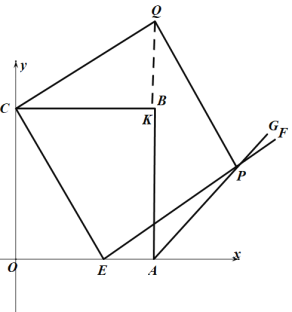
∵四边形是正方形,
∴![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (此时K与点B重合),
(此时K与点B重合),
![]() ,
,
![]() .
.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】观察下面的表格,根据表格解答下列问题:
| -2 | 0 | 1 |
| 1 | ||
| -3 | -3 |
(1)写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)在直角坐标系中画出二次函数![]() 的图象;并根据图象写出使不等式
的图象;并根据图象写出使不等式![]() 成立时
成立时![]() 的取值范围;
的取值范围;
(3)设该图象与![]() 轴两个交点分别为
轴两个交点分别为![]() ,
,![]() ,与
,与![]() 轴交点为
轴交点为![]() ,直接写出
,直接写出![]() 的外心坐标.
的外心坐标.

【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
表1:四种款式电脑的利润
电脑款式 | A | B | C | D |
利润(元/台) | 160 | 200 | 240 | 320 |
表2:甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量(台) | 20 | 15 | 10 | 5 |
乙店销售数量(台)8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识,解决下列问题:
(1)从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为 ;
(2)经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.