题目内容
2.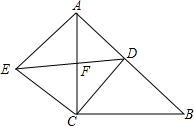 已知如图,△ABC是等腰三角形,∠ACB=90°,D是斜边AB上的一动点,联结CD,线段CD绕点C逆时针旋转90°,点D与点E重合,联结AE,DE,线段DE交边AC于点F.
已知如图,△ABC是等腰三角形,∠ACB=90°,D是斜边AB上的一动点,联结CD,线段CD绕点C逆时针旋转90°,点D与点E重合,联结AE,DE,线段DE交边AC于点F.(1)求证:AE=BD;
(2)点D在边AB上运动的过程中,△AEF是否可能为等腰三角形?若不能,请说明理由;若可能,请写出此时∠BCD的度数.
分析 (1)先证明AB=BC,CE=CD以及∠ACE=∠BCD,即可证明△ACE≌△BCD,则AE=BD;
(2)可能,若△AEF是等腰三角形,则∠ECF=∠DCB=90°-45°=45°.
解答 (1)证明:∵△ABC是等腰三角形,
∴AC=BC,
∵线段CD绕点C逆时针旋转90°,点D与点E重合,
∴CE=CD,∠DCE=90°,
∵∠ACE=∠DCE-∠ACD=90°-∠ACD,
∠BCD=∠ACB-∠ACD=90°-∠ACD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴AE=BD;
(2)解:能.
由(1)可知∠EAC=∠B=45°,∠ECF=∠DCB,
∵△AEF是等腰三角形,
∴AF=EF,∠EAF=∠AEF=45°,
∴EF⊥AC,∠EFC=∠EFA=90°,
∵EC=CD,∠ECD=90°,
∴∠DEC=∠EDC=45°,
∴∠ECF=∠DCB=90°-45°=45°.
点评 本题主要考查了全等三角形的判定与性质以及等腰直角三角形的性质,证明△ACE≌△BCD是解决问题的关键.

练习册系列答案
相关题目
7.在某次实验中,“蛟龙号”载人潜水器停在海面下5000米处,先下降2062米,又上升1300米,这是“蛟龙号”载人潜水器停在海面下( )
| A. | 4362米处 | B. | 4762米处 | C. | 5362米处 | D. | 5762米处 |
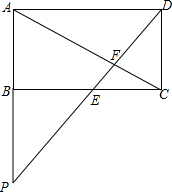 如图,已知四边形ABCD是矩形,求证:DF2=EF•FP.
如图,已知四边形ABCD是矩形,求证:DF2=EF•FP.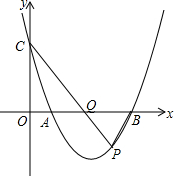 已知抛物线y=$\frac{3}{4}$x2-$\frac{15}{4}$x+3交x轴于A、B点,交y轴于点C,点P为x轴下方抛物线上一点,CP交x轴于点Q,当S△ACQ=S△PBQ,求点P的坐标.
已知抛物线y=$\frac{3}{4}$x2-$\frac{15}{4}$x+3交x轴于A、B点,交y轴于点C,点P为x轴下方抛物线上一点,CP交x轴于点Q,当S△ACQ=S△PBQ,求点P的坐标. 如图,△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC在O点的同侧,且对应边之比为2:1,试写出△DEF各项点的坐标.
如图,△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC在O点的同侧,且对应边之比为2:1,试写出△DEF各项点的坐标.