题目内容
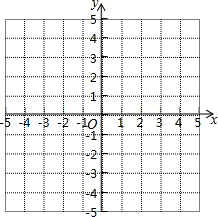 已知在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).
已知在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).(1)将△ABC先向左平移3个单位长度,再向下平移4个单位长度得到△A1B1C1,请写出A1,B1,C1三个点的坐标,并在图上画出△A1B1C1;
(2)求△A1B1C1的面积.
(3)若点D在过点B1且平行于x轴的直线上,且△A1B1D的面积等于△A1B1C1的面积,请直接写出点D的坐标.
分析:(1)画出图形,根据各点在坐标系中的位置写出A1,B1,C1三个点的坐标即可;
(2)过点C1作C1M⊥A1B1于点M,根据三角形的面积公式即可得出结论;
(3)根据△A1B1D的面积等于△A1B1C1的面积找出D点,得出其坐标即可.
(2)过点C1作C1M⊥A1B1于点M,根据三角形的面积公式即可得出结论;
(3)根据△A1B1D的面积等于△A1B1C1的面积找出D点,得出其坐标即可.
解答: 解:(1)如图所示:
解:(1)如图所示:
A1(-2,0),B1(-2,-3),C1(0,-2);
(2)过点C1作C1M⊥A1B1于点M,
则S△A1B1C1=
A1B1×C1M=
×3×2=3;
(3)由图可知,D1(-4,-3 ) D2(0,-3).
 解:(1)如图所示:
解:(1)如图所示:A1(-2,0),B1(-2,-3),C1(0,-2);
(2)过点C1作C1M⊥A1B1于点M,
则S△A1B1C1=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由图可知,D1(-4,-3 ) D2(0,-3).
点评:本题考查的是作图-平移变换,熟知图形平移的性质是解答此题的关键.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.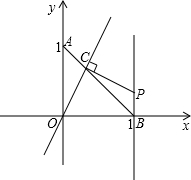 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.