��Ŀ����
һ�κ���y=ax+b��ͼ��ֱ���x�ᣬy�ύ�ڵ�M��N���뷴��������y=| k |
| x |
��1������A��B�ڷ���������y=
| k |
| x |
��2������A��B�ֱ��ڷ���������y=
| k |
| x |

��������1��������������AD��BC���ó�S��ADC=S��BDC��֤��ANDC��ƽ���ı��Σ��ó�AN=CD��DC=BM���Ӷ��ó�AN=BM��
��2���������ȸ��ݣ�1�������ɼ��ɵó�AN��BM��ȼ��ɣ�
��2���������ȸ��ݣ�1�������ɼ��ɵó�AN��BM��ȼ��ɣ�
����⣺��1������AD��BC����D��DP��AB����C��CQ��AB��
S��ADC=
AC��DK=
x1��y1=
k��
S��BDC=
BD��CK=
x2y2=
k��
��S��ADC=S��BDC����S��ADK=S��BCK��
��S��ADB=S��ACB��
��DP=CQ����DP��CQ���֡�DPQ=90�㣬
���ı���PQCDΪ���Σ�
��AB��CD��
��AC��ND��
��ANDC��ƽ���ı��Σ�
��AN=CD��
ͬ����DC=BM��
��AN=BM��

��2����ȣ�
AN��BM��Ȼ��ȣ�
��S����AEDK=S����AEOC+S����ODKC��S����BKCF=S����BDOF+S����ODKC��
�֡�S����AEOC=S����BDOF=k��
��S����AEDK=S����BKCF��
��AK•DK=BK•CK��
��CK��AK=DK��BK��
�ߡ�K=��K��
���CDK�ס�ABK��
���CDK=��ABK��
��AB��CD
��AC��y�ᣬ
���ı���ANDC��ƽ���ı��Σ�
��AN=CD��
ͬ��BM=CD��
��AN=BM��
S��ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S��BDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��S��ADC=S��BDC����S��ADK=S��BCK��
��S��ADB=S��ACB��
��DP=CQ����DP��CQ���֡�DPQ=90�㣬
���ı���PQCDΪ���Σ�
��AB��CD��
��AC��ND��
��ANDC��ƽ���ı��Σ�
��AN=CD��
ͬ����DC=BM��
��AN=BM��

��2����ȣ�
AN��BM��Ȼ��ȣ�
��S����AEDK=S����AEOC+S����ODKC��S����BKCF=S����BDOF+S����ODKC��
�֡�S����AEOC=S����BDOF=k��
��S����AEDK=S����BKCF��
��AK•DK=BK•CK��
��CK��AK=DK��BK��
�ߡ�K=��K��
���CDK�ס�ABK��
���CDK=��ABK��
��AB��CD
��AC��y�ᣬ
���ı���ANDC��ƽ���ı��Σ�
��AN=CD��
ͬ��BM=CD��
��AN=BM��
������������Ҫ�����˷������������ۺ�Ӧ�ã��ڽ���ʱҪ�ܰѷ�����������ͼ����ƽ���ı��ε��ж������������DZ���Ĺؼ���

��ϰ��ϵ�д�
 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
�����Ŀ
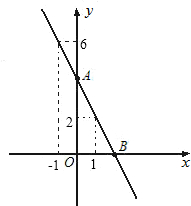 ��֪��ͼ��һ�κ���y=ax+bͼ���㣨1��2�����㣨-1��6������
��֪��ͼ��һ�κ���y=ax+bͼ���㣨1��2�����㣨-1��6������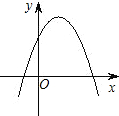 ��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������ͬһ����ϵ�У�һ�κ���y=ax+c�ͷ���������y=
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������ͬһ����ϵ�У�һ�κ���y=ax+c�ͷ���������y=
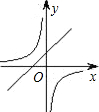
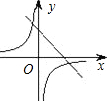
 ��ͼ��һ�κ���y=ax+b��ͼ���뷴��������y=
��ͼ��һ�κ���y=ax+b��ͼ���뷴��������y=