Question

【题目】如图，在△ABC和△ACD中，∠B=∠D，tanB=，BC=5，CD=3，∠BCA=90°﹣∠BCD，则AD=_____．

Answer 1

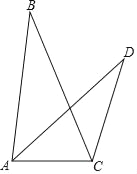
【答案】

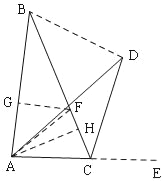
【解析】解：在BC上取一点F，使BF=CD=3，连接AF，

∴CF=BC﹣BF=5﹣3=2，

过F作FG⊥AB于G，

∵tanB== ，

设FG=x，BG=2x，则BF=x，

∴x=3，

x=，

即FG=，

延长AC至E，连接BD，

∵∠BCA=90°﹣∠BCD，

∴2∠BCA+∠BCD=180°，

∵∠BCA+∠BCD+∠DCE=180°，

∴∠BCA=∠DCE，

∵∠ABC=∠ADC，

∴A、B、D、C四点共圆，

∴∠DCE=∠ABD，∠BCA=∠ADB，

∴∠ABD=∠ADB，

∴AB=AD，

在△ABF和△ADC中，

∵ ,

∴△ABF≌△ADC（SAS），

∴AF=AC，

过A作AH⊥BC于H，

∴FH=HC=FC=1，

由勾股定理得：AB2=BH2+AH2=42+AH2①，

S△ABF=ABGF=BFAH，

∴AB=3AH，

∴AH=，

∴AH2=②，

把②代入①得：AB2=16+，

解得：AB=，

∵AB＞0，

∴AD=AB=2，