Question

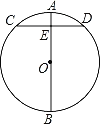
【题目】如图，△ABC内接于⊙O，直径DE⊥AB于点F，交BC于点 M，DE的延长线与AC的延长线交于点N，连接AM．

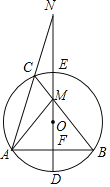
（1）求证：AM＝BM；

（2）若AM⊥BM，DE＝8，∠N＝15°，求BC的长．

Answer 1

【答案】（1）见解析；（2）+

【解析】

（1）由垂径定理可求得AF＝BF，可知DE为AB的垂直平分线，可得AM＝BM；

（2）连接AO，BO，可求得∠ACB＝60°，可求得∠AOF，由DE的长可知AO，在Rt△AOF中得AF，在Rt△AMF中可求得AM，在Rt△ACM中，由，可求得CM，则可求得BC的长．

（1）证明：

∵直径DE⊥AB于点F，

∴AF＝BF，

∴AM＝BM；

（2）连接AO，BO，如图，

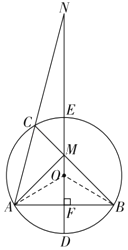
由（1）可得 AM＝BM，

∵AM⊥BM，

∴∠MAF＝∠MBF＝45°，

∴∠CMN＝∠BMF＝45°，

∵AO＝BO，DE⊥AB，

∴∠AOF＝∠BOF＝，

∵∠N＝15°，

∴∠ACM＝∠CMN+∠N＝60°，即∠ACB＝60°，

∵∠ACB＝．

∴∠AOF＝∠ACB＝60°．

∵DE＝8，

∴AO＝4．

在Rt△AOF中，由，得AF＝，

在Rt△AMF中，AM＝＝．得BM= AM＝，

在Rt△ACM中，由，得CM＝，

∴BC＝CM+BM＝+．