Question

【题目】如图，直线y= x﹣ 与x，y轴分别交于点A，B，与反比例函数y= （k＞0）图象交于点C，D，过点A作x轴的垂线交该反比例函数图象于点E．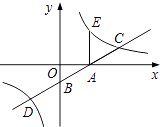
（1）求点A的坐标．
（2）若AE=AC． ①求k的值．
②试判断点E与点D是否关于原点O成中心对称？并说明理由．

Answer 1

【答案】
（1）解：当y=0时，得0= x﹣ ，解得：x=3．

∴点A的坐标为（3，0）．

（2）解：①过点C作CF⊥x轴于点F，如图所示．

设AE=AC=t，点E的坐标是（3，t），

在Rt△AOB中，tan∠OAB= = ，

∴∠OAB=30°．

在Rt△ACF中，∠CAF=30°，

∴CF= t，AF=ACcos30°= t，

∴点C的坐标是（3+ t， t）．

∴（3+ t）× t=3t，

解得：t1=0（舍去），t2=2 ．

∴k=3t=6 ．

②点E与点D关于原点O成中心对称，理由如下：

设点D的坐标是（x， x﹣ ），

∴x（ x﹣ ）=6 ，解得：x1=6，x2=﹣3，

∴点D的坐标是（﹣3，﹣2 ）．

又∵点E的坐标为（3，2 ），

∴点E与点D关于原点O成中心对称．

【解析】（1）令一次函数中y=0，解关于x的一元一次方程，即可得出结论；（2）①过点C作CF⊥x轴于点F，设AE=AC=t，由此表示出点E的坐标，利用特殊角的三角形函数值，通过计算可得出点C的坐标，再根据反比例函数图象上点的坐标特征可得出关于t的一元二次方程，解方程即可得出结论；②根据点在直线上设出点D的坐标，根据反比例函数图象上点的坐标特征可得出关于点D横坐标的一元二次方程，解方程即可得出点D的坐标，结合①中点E的坐标即可得出结论．